摘要
对于非线性动力系统而言,识别其控制方程是理解系统物理特性并构建精确动力学模型的关键。然而,在多数实际场景中,系统往往只能提供部分可观测数据,这为系统辨识带来了显著挑战。针对这一问题,研究团队提出了一种专为部分观测条件设计的机器学习框架,能够有效实现系统状态重构与动力学建模的联合求解。

关键词:部分观测非线性动力系统、系统识别、机器学习、可解释符号模型

论文题目:Discovering sparse interpretable dynamics from partial observations
发表时间:2022年8月12日
发表期刊:Nature Communications:Physics
论文链接:https://www.nature.com/articles/s42005-022-00987-z

挑战与困境
在部分观测条件下对非线性动力系统进行研究时,研究人员不仅需要准确识别系统的动态行为,还需同时重构未被直接观测到的隐藏状态变量,这构成了系统辨识中的核心难题。
传统线性系统辨识方法难以应对非线性系统的复杂性,性能受限;而尽管深度学习模型具备强大的拟合能力,但其“黑箱”属性严重削弱了模型的可解释性,无法揭示潜在的物理机制。这些方法上的局限进一步加大了从有限观测中恢复完整系统结构的难度。
为解决上述问题,MIT物理系的研究团队开发出一种新型机器学习框架。该框架创新性地融合了全状态重构编码器与稀疏符号模型——后者直接学习系统的控制方程,并通过匹配高阶时间导数完成训练。此外,该方法允许将已知的物理约束嵌入编码器结构与符号模型设计中,从而灵活适配不同类型的非线性系统,显著提升了模型的适应性与效率。
特别地,作者设计了一种算法技巧,使得标准自动微分技术可用于计算高阶符号时间导数,增强了训练过程的稳定性与可行性。

部分观测非线性系统的机器学习识别
问题形式化描述
考虑一个由一阶常微分方程描述的动力系统:
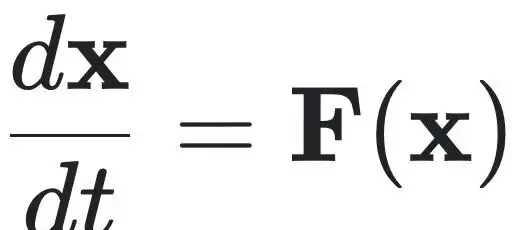
其中,观测到的状态 $ x_v = g(x) $ 是完整状态 $ x $ 的投影,而隐藏状态 $ x_h $ 需通过聚合函数 $ a(\cdot,\cdot) $ 构造,且满足 $ a(x_v, x_h) = x $。目标是在不完全观测下,同步重构隐藏状态 $ x_h $ 并识别控制整个系统演化的动力学函数 $ F $。
当缺乏先验知识时,通常假设可见状态 $ x_v = (x_1, x_2, \dots, x_k) $ 是完整状态 $ x = (x_1, x_2, \dots, x_n) $ 的子集,此时 $ g $ 表示投影操作,隐藏状态 $ x_h = (x_{k+1}, \dots, x_n) $,而聚合函数 $ a $ 简单地执行拼接操作。
若存在关于系统结构的先验信息,则可选择更合适的投影函数 $ g $ 和聚合函数 $ a $,以更好地反映真实动力学结构。
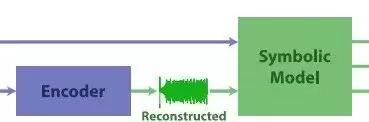
框架构成
该机器学习框架由两个关键模块组成:编码器(Encoder)和可解释的稀疏符号模型(Symbolic Model)。前者负责从观测序列中重建隐藏状态,后者用于发现系统的控制方程 $ F $。
编码器 $ e_\eta $ 通常采用具有可学习参数 $ \eta $ 的神经网络,输入为可见状态序列:
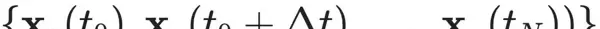
输出为对应的隐藏状态序列估计值:
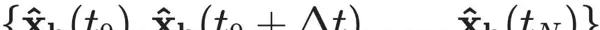
基于塔肯斯嵌入定理(Takens’ embedding theorem),只要隐藏状态与可观测状态之间存在充分耦合,这种重构在理论上是可行的。随后,利用聚合函数:
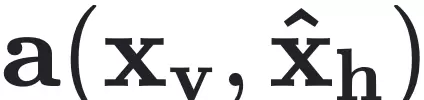
得到完整的状态重构结果 $ \hat{x} $。该重构状态可用于计算由符号模型定义的时间导数:

其中符号模型的形式为:
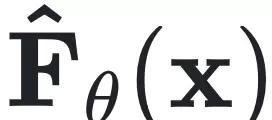
这里 $ f_1, f_2, \dots, f_m $ 是预设的候选函数项,$ \theta_1, \theta_2, \dots, \theta_m $ 是待学习的系数。当系统维度未知时,可通过调整候选项数量这一超参数,在模型精度与简洁性之间取得平衡。
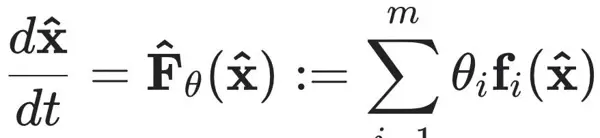
训练策略
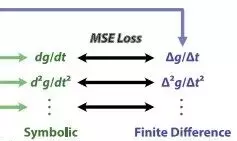
整个模型的训练基于最小化均方误差(MSE)损失函数,该函数综合考虑了多个阶次的时间导数信息,并引入经验方差与权重超参数,对各阶有限差分近似进行加权校准,确保训练过程的鲁棒性和准确性。
整体训练流程采用联合优化方式,同步更新编码器与符号模型参数,从而实现状态重构与动力学识别的协同提升。
损失函数定义如下:
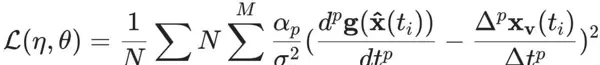
其中,
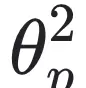
表示第 $ p $ 阶有限差分导数的估计,$ a_p $ 为对应阶数的权重超参数,用于调节不同阶导数在损失中的贡献程度。
损失函数中的关键项
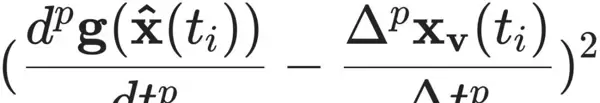
体现了仅依赖部分观测数据进行联合训练的设计思想。其中
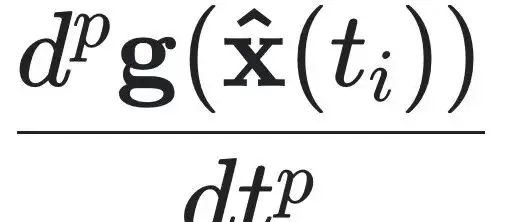
是由符号模型隐式生成的可见状态
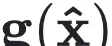
的高阶符号时间导数,同样由模型

所定义。
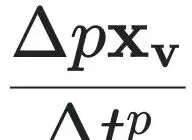
图3展示了符号时间导数、有限差分导数与MSE损失之间的关系,直观呈现了训练过程中多阶导数匹配的核心机制。
在数据处理中,采用了有限差分法进行导数估计,以支持模型对动态系统行为的学习与识别。
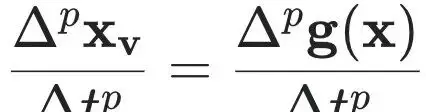
符号模型的稀疏化策略
为了实现符号模型结构上的稀疏性,研究团队引入了一种常用于稀疏线性回归中的阈值处理方法。具体而言,在训练过程中会周期性地检查可学习参数 θi 的数值大小;若其绝对值低于预设的阈值,则将该系数强制置零,从而增强模型的简洁性和可解释性。
数值实验设计与性能评估
为全面验证所提出机器学习框架的有效性,研究团队设计并实施了三类系统的数值实验,涵盖常微分方程、偏微分方程以及复杂物理系统的相位重构任务。
常微分方程系统实验
实验选取了两个经典的混沌非线性动力系统作为测试对象:罗塞尔系统(Rssler system)和洛伦兹系统(Lorenz system)。实验结果表明,该框架不仅能准确识别出系统的控制方程,还能有效重构被隐藏的状态变量,展现出其在常微分方程建模中的高精度与强泛化能力。
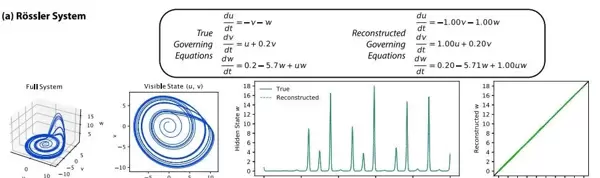
图4:ODE实验 — 罗塞尔系统
可见变量为 u 和 v,隐藏变量为 w。图中展示了三维动力学轨迹及其在可见状态 (u, v) 平面上的投影;同时,真实隐藏状态 w(蓝色曲线)与重建结果(绿色虚线)随时间的变化趋势被清晰呈现,并通过绿色散点图进行直接对比。
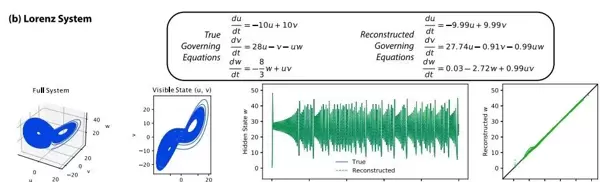
图5:ODE实验 — 洛伦兹系统
可见变量为 u 和 v,隐藏变量为 w。图中包含三维轨迹及 (u, v) 投影视图;真实状态(蓝色)与重建状态(绿色虚线)对应的隐藏变量 w 随时间演化的轨迹被并列展示,并辅以散点图形式直观比较两者的吻合程度。
偏微分方程系统实验
为进一步验证框架在空间扩展系统中的适用性,研究团队将其应用于两类偏微分方程系统:一是带有指数衰减源项的二维扩散系统(2D diffusion system),二是二维扩散型洛特卡–沃尔泰拉捕食者–猎物系统(2D diffusive Lotka–Volterra predator–prey system)。
实验结果显示,该方法在这两种复杂场景下均能成功识别出系统的控制方程,并精确重构出隐藏的空间组分,证明了其在处理高维、非线性偏微分系统时依然具备良好的适应性和鲁棒性。
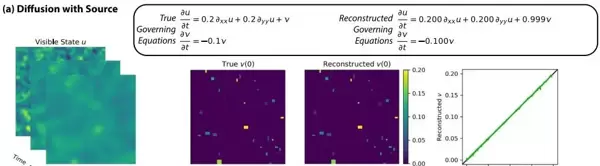
图6:PDE实验 — 二维扩散系统
u 为可观测变量,v 为待重构的隐藏变量。图像内容包括可见状态 u 随时间演化的快照;在 t = 0 时刻同步显示真实状态 v 与重构状态 v 的分布情况,并通过对比图清晰展示两者之间的相似度。
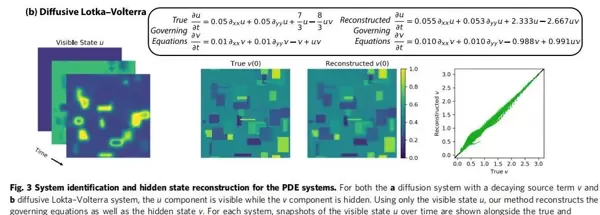
图7:PDE实验 — 扩散型洛特卡–沃尔泰拉系统
u 为可见变量,v 为隐藏变量。图示包含 u 的时间演化快照;t = 0 时刻的真实 v 与重构 v 被同时呈现,并通过对比图直观反映重建效果。
一维非线性薛定谔方程的相位重构实验
研究还拓展至量子物理相关领域,针对一维非线性薛定谔方程开展相位重构实验。在此任务中,仅提供可见的振幅信息
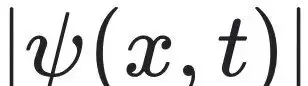
目标是从这些观测数据中识别潜在的动力学规律,并恢复隐藏的相位信息

基于先验知识,作者设定了投影函数的形式
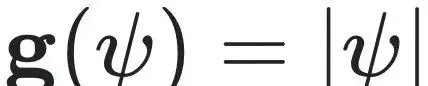
以及聚合函数的结构
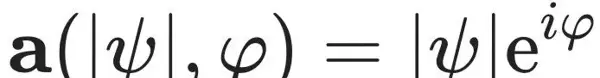
由于传统的局部时空编码器难以直接完成相位重构,研究人员为每个时空点独立学习一个对应的相位参数
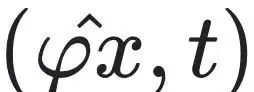
为缓解由此带来的优化难度,引入了一个编码器正则化项
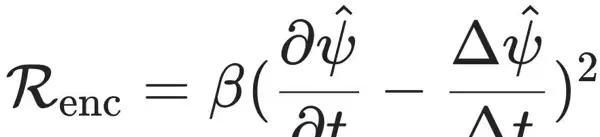
用以约束符号时间导数与重构状态之间的一致性,确保训练过程稳定收敛
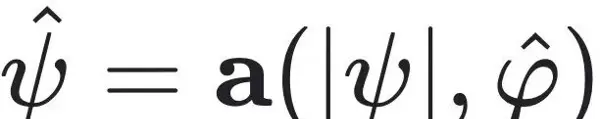
实验结果表明,该方法成功识别出了非线性薛定谔方程的核心控制方程,并基本还原了正确的相位分布模式。此外,研究指出,利用本框架提取出的解析方程,后续可结合更专业的非线性相位恢复算法进行后处理,进一步提升重建质量,这也为实际应用提供了可行的技术路径。
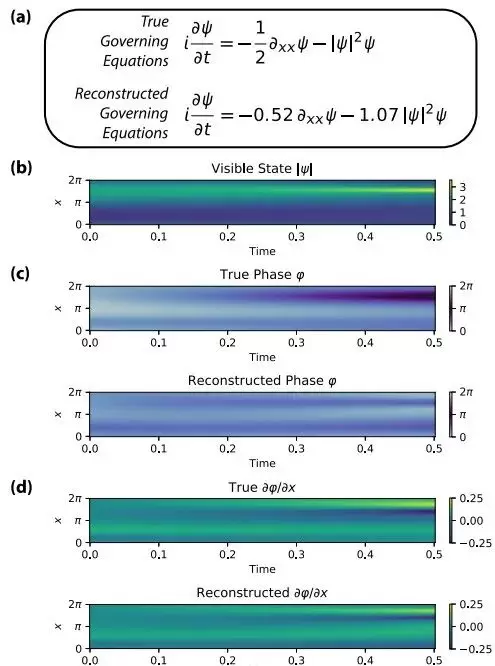
图8:非线性薛定谔系统的系统识别与相位重建
a. 本文方法成功识别出正确的非线性薛定谔方程;
b. 可见变量为波函数的模 |ψ|;
c. 需要重构的隐藏变量为相位 φ = arg(ψ);
d. 展示了相位的空间导数及其重建结果。
讨论与未来展望:优势、局限与发展方向
本研究提出了一种新颖的机器学习框架,能够在部分观测条件下同步实现稀疏、可解释的动力学规律识别与隐藏状态重构。该方法结构简洁、灵活性强,相较于依赖显式数值积分的传统方法,具有更高的计算效率,为非线性动力系统的建模提供了一条新的技术路线。
然而,当前方法的一个主要局限在于其对噪声较为敏感,原因在于其依赖于数据中高阶有限差分来估计时间导数,而这类操作在含噪环境下容易放大误差。
未来工作将聚焦于改进现有框架,计划融入能够联合识别动力学规律与噪声统计特性的新机制,并探索适用于符号回归任务的多层可组合符号模型结构,以增强模型在真实噪声环境下的稳定性与实用性。
现已收录超过8000篇重要文献资料,涵盖广泛的研究领域。
每周持续更新,新增不少于100篇来自全球的最新研究成果。


 扫码加好友,拉您进群
扫码加好友,拉您进群