优化｜PyOptInterface:高效且灵活的Python优化建模语言

230

收藏 2025-11-28

编者按：作为连接优化求解器与终端用户的桥梁，优化建模语言在构建、求解和分析各类优化模型中起着关键作用。其建模效率直接影响整个优化流程的执行时间。PyOptInterface 是一种基于 Python 的新型开源建模语言，在保持灵活性的同时显著提升了建模性能，相比现有工具实现了 10-20 倍的速度提升。

一、PyOptInterface 概述

PyOptInterface 是由合肥工业大学电气与自动化工程学院杨越副教授与清华大学电机系吴文传教授团队联合开发的一款基于 Python 的开源通用优化建模语言。项目代码已发布于 GitHub 平台：https://github.com/metab0t/PyOptInterface，并配有完整的在线文档支持：https://metab0t.github.io/PyOptInterface/。相关研究成果也已发表在 arXiv 预印本平台：https://arxiv.org/abs/2405.10130。

该语言目前支持以下八类主流优化问题类型：

线性规划 (LP)
混合整数线性规划 (MILP)
二次规划 (QP)
混合整数二次规划 (MIQP)
二次约束二次规划 (QCQP)
混合整数二次约束二次规划 (MIQCQP)
二阶锥规划 (SOCP)
混合整数二阶锥规划 (MISOCP)

在求解器兼容性方面，PyOptInterface 可调用以下四款高性能商业及开源优化求解器：

COPT
Gurobi
HiGHS
Mosek

二、当前优化建模面临的挑战

尽管已有 AMPL、GAMS、Pyomo、JuMP.jl 等多求解器兼容的通用建模语言，以及 COPT、Gurobi 自带的 Python 接口，但在实际应用过程中仍存在若干瓶颈：

AMPL 和 GAMS 属于领域特定语言（DSL），学习成本较高，难以融入以 Python 为主的数据分析工作流，且不便于实现高效的模型增量更新与迭代求解。
以 Pyomo 为代表的多求解器建模语言，在处理大规模模型时建模速度较慢，与直接调用求解器底层接口相比存在明显性能差距。
虽然 COPT、Gurobi 等求解器提供的原生 Python 接口性能良好，但各求解器接口设计差异大，导致代码高度依赖特定求解器，迁移和切换困难。

三、PyOptInterface 的核心优势

PyOptInterface 采用创新架构设计，通过高效映射变量、约束等对象与求解器底层接口之间的关系，极大缩小了通用建模语言与底层 C/C++ 接口之间的性能鸿沟。相较于现有方案，具备以下突出优点：

内核使用 C++ 实现，并直接调用求解器的底层 C 接口，建模速度接近原生 C++ 调用水平。实测中比 Pyomo 快 10-20 倍，优于部分官方 Python 接口 2-5 倍，甚至超越当前最快的开源建模语言 JuMP.jl。
支持对模型进行动态增量修改并重新求解，包括添加、删除或修改变量与约束，调整目标函数等操作，无需重建模型，适用于 Benders 分解、列生成、序列线性化等需多次迭代求解的算法场景。
提供统一的编程接口，用户只需编写一套代码即可无缝运行于多个不同求解器之上，提升开发效率与可移植性。
在统一接口基础上，仍保留对求解器特有参数的配置能力及高级功能支持，例如 MIP 求解过程中的回调函数（callback function），功能完备性接近各求解器官方 Python 接口。

四、建模性能对比测试

为验证性能表现，选取八个不同规模的典型优化模型，分别以 Gurobi 和 COPT 作为后端求解器进行两轮基准测试。所有测试均记录从模型构建到提交求解器的总耗时，并将求解时间限制设为 0.0 秒，以排除求解阶段干扰，仅聚焦建模效率。

下表展示了使用不同建模语言将模型提交至 Gurobi 求解器所需的时间（单位：秒）：

Model	Variables	C++	PyOptInterface	JuMP	gurobipy	Pyomo
fac-25	67651	0.2	0.2	0.2	1.2	4.1
fac-50	520301	0.8	1.2	1.8	9.7	32.7
fac-75	1732951	2.7	4.1	6.6	32.5	119.3
fac-100	4080601	6.3	10.0	17.8	79.1	286.3
lqcp-500	251501	0.9	1.5	1.3	6.3	23.8
lqcp-1000	1003001	3.7	6.0	6.1	26.7	106.6
lqcp-1500	2254501	8.3	14.0	17.7	61.8	234.0
lqcp-2000	4006001	14.5	24.9	38.3	106.9	444.1

测试结果表明，PyOptInterface 在建模效率上显著优于主流建模语言，尤其在处理大规模模型时优势更为明显。

五、安装与使用说明

PyOptInterface 已在 PyPI 平台正式发布，兼容 Windows、Linux 和 macOS 操作系统，支持 Python 3.8 至 3.12 的所有版本。用户可通过 pip 命令直接进行安装：

pip?install pyoptinterface

完成安装后，即可在 Python 脚本中导入该模块以开始使用：

import?pyoptinterfaceaspoi

PyOptInterface 本身不依赖任何第三方库，但若需连接特定优化求解器，则需手动安装对应的求解器程序。具体配置步骤可参考官方文档（https://metab0t.github.io/PyOptInterface/getting_started.html）中的详细指南。

此外，PyOptInterface 提供了对开源求解器 HiGHS 的集成安装方式：

pip install pyoptinterface[highs]

执行上述命令将自动安装 HiGHS 的二进制版本，便于与 PyOptInterface 直接协同运行。

附录：快速入门教程

以下以一个基础线性规划问题为例进行说明：

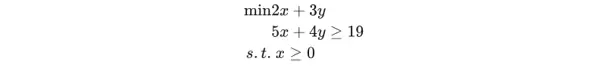
import pyoptinterface as poi
from pyoptinterface import copt

model = copt.Model()

x = model.add_variable(lb=0, name="x")
y = model.add_variable(lb=0, ub=10, name="y")
con = model.add_linear_constraint(5*x+4*y, poi.Geq, 19)
model.set_objective(2*x+3*y)
model.optimize()
x_value = model.get_value(x)
y_value = model.get_value(y)

首先创建一个模型实例，然后通过调用 model.add_variable 方法添加决策变量，并可设定其上下界及命名。接着使用 model.add_linear_constraint 添加线性约束，利用 model.set_objective 定义目标函数。得益于运算符重载机制，线性表达式可通过变量的常规四则运算直接构造。最后调用 model.optimize 启动求解过程，并通过 model.get_value 获取变量的最优值。

若需引入整数变量，可将原问题扩展为混合整数线性规划问题。此时，在调用 add_variable 时指定变量类型为整数即可：

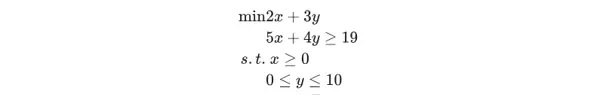
import pyoptinterface as poi
from pyoptinterface import copt

model = copt.Model()

x = model.add_variable(lb=0, domain=poi.VariableDomain.Integer, name="x")
y = model.add_variable(lb=0, ub=10, domain=poi.VariableDomain.Integer, name="y")
con = model.add_linear_constraint(5*x+4*y, poi.Geq, 19)
model.set_objective(2*x+3*y)
model.optimize()

x_value = model.get_value(x)
y_value = model.get_value(y)

若进一步将目标函数改为二次形式，则问题转化为混合整数二次规划问题，仅需调整目标函数定义部分：

import pyoptinterface as poi
from pyoptinterface import copt

model = copt.Model()

x = model.add_variable(lb=0, domain=poi.VariableDomain.Integer, name="x")
y = model.add_variable(lb=0, ub=10, domain=poi.VariableDomain.Integer, name="y")
con = model.add_linear_constraint(5*x+4*y, poi.Geq, 19)
model.set_objective(2*x*x+3*y*y)
model.optimize()

x_value = model.get_value(x)
y_value = model.get_value(y)

最后，展示一个使用 PyOptInterface 求解经典 8 皇后问题的案例。通过构建一个 8×8 的 0-1 变量矩阵，并将其建模为混合整数线性规划问题，结合 HiGHS 求解器寻找可行解，最终输出棋盘布局。示例中采用 NumPy 多维数组存储变量对象，体现了 PyOptInterface 与 Python 生态系统中其他第三方库的良好兼容性。

import numpy as np
import pyoptinterface as poi
from pyoptinterface import highs

model = highs.Model()

N = 8

x = np.empty((N, N), dtype=object)
for?i?in?range(N):
? ??for?j?in?range(N):
? ? ? ? x[i, j] = model.add_variable(domain=poi.VariableDomain.Binary)

for?i?in?range(N):
? ??# 行列约束
? ? model.add_linear_constraint(poi.quicksum(x[i, :]), poi.Eq, 1.0)
? ? model.add_linear_constraint(poi.quicksum(x[:, i]), poi.Eq, 1.0)
for?i?in?range(-N+1, N):
? ??# 对角线约束
? ? model.add_linear_constraint(poi.quicksum(x.diagonal(i)), poi.Leq, 1.0)
model.add_linear_constraint(poi.quicksum(np.fliplr(x).diagonal(i)), poi.Leq, 1.0)

model.optimize()

get_v = np.vectorize(lambda x: model.get_value(x))
x_value = get_v(x)

print(x_value.astype(int))

表2：生成优化模型并提交至 COPT 求解器所耗时间（单位：秒）

Model	Variables	C++	PyOptInterface	JuMP	coptpy	Pyomo
fac-25	67651	0.3	0.2	0.3	0.6	4.1
fac-50	520301	2.2	1.5	2.7	5.4	32.8
fac-75	1732951	8.1	6.6	10.2	20.3	117.4
fac-100	4080601	22.4	23.4	30.3	58.0	284.0
lqcp-500	251501	3.8	3.1	3.0	6.6	26.4
lqcp-1000	1003001	16.0	15.5	13.9	28.1	112.1
lqcp-1500	2254501	37.6	32.4	33.7	64.6	249.3
lqcp-2000	4006001	68.2	60.3	66.2	118.4	502.4

六、总结与展望

目前，PyOptInterface 已在电力系统优化等多个实际领域开展试点应用。欢迎广大研究人员和开发者在学术研究及相关项目中积极尝试使用本工具。软件遵循 Mozilla Public License Version 2.0 开源协议，允许自由使用、修改与分发。

扫码加我拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝