一、KNN的基本概念

KNN（K-Nearest Neighbors）是一种典型的基于实例的监督学习方法，广泛应用于分类与回归任务中。该算法在预测时并不立即进行建模，而是依赖于已有的训练样本集，通过比对新样本与已有样本之间的相似度来进行结果推断。

二、KNN的核心原理

其核心理念可概括为“近朱者赤，近墨者黑”，即一个未知样本的类别或数值可以通过它周围最邻近的K个已知样本的标签来决定。对于分类问题，采用多数投票法；而对于回归问题，则取这K个邻居目标值的平均数作为预测输出。

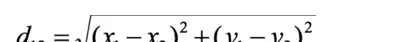
三、KNN的应用场景

该算法适用于多种实际问题：

• 分类任务：如鸢尾花种类识别、垃圾邮件判断等。
• 回归任务：例如房价估算、气温预测等连续值输出问题。

四、常用的距离度量方式

在KNN中，衡量样本间“远近”的关键在于距离的计算方式，常见的包括以下几种：

欧式距离：也称L2距离，代表空间中两点间的直线距离。

通俗理解：各维度差值平方和再开根号。

这是KNN默认使用的距离公式。

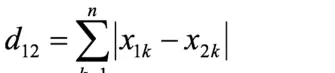
曼哈顿距离：又称城市街区距离或L1距离，模拟只能沿坐标轴方向移动的情形。

通俗理解：各维度差值绝对值之和。

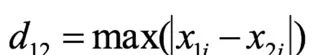
切比雪夫距离：允许水平、垂直及45度斜向移动，类似于国际象棋中国王的走法。

通俗理解：所有维度差值绝对值中的最大值。

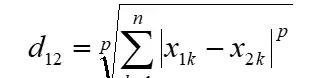
闵可夫斯基距离：是上述多种距离的统一形式，具有通用性。

当参数 p=1 时，退化为曼哈顿距离；
当 p=2 时，对应于欧式距离；
当 p 趋向无穷大时，则等价于切比雪夫距离。

五、KNN在分类任务中的实现流程

1. 计算待预测样本与每个训练样本之间的距离。
2. 选取距离最小的K个近邻样本。
3. 对这K个样本的类别标签进行投票统计。
4. 将得票最多的类别作为最终预测结果。

'''
步骤：
    1- 加载数据
    2- 数据预处理
    3- 特征工程
    4- 模型巡礼那
    5- 模型评估
    6- 模型测试
'''
from sklearn.neighbors import KNeighborsClassifier   # KNN分类算法的API
# 1.加载数据
x_train = [[1],[2],[3],[4]] # 训练集的特征
y_train = [0,0,1,1]         # 训练集的标签
x_test = [[5]]              # 测试集的特征

# 2.数据预处理--->此处不需要

# 3.特征工程--->此处不需要

# 4.模型训练
'''
主要参数：
n_neighbors=5:K的个数，默认是5。
metric="minkowski":距离公式，默认选择的是闵式距离
p=2:默认是2，当选择2之后，和第二个参数进行合并的话 就是选择的是欧式距离

当距离公式选择的是闵式距离之后，当p=2,代表欧式距离
当距离公式选择的是闵式距离之后，当p=1,代表曼哈顿距离（城市街区距离）
当距离公式选择的是闵式距离之后，当p=??,代表切比雪夫距离

欧式距离：对应维度值的差的平方和开平方根（类似与勾股定理）
曼哈顿距离（城市街区距离）：对应维度值的差的绝对值的和
切比雪夫距离：对应维度值的差的最大值
'''
# 这句代码只是创建出来了模型，就好像是创建出来汽车外架了，但是发动机什么的都没有
model = KNeighborsClassifier(n_neighbors = 2,metric='minkowski',p=2) # 模型使用的是KNN分类模型，K是2，距离是欧式距离
model.fit(x_train,y_train) # 这句话的意思是使用训练集的特征和标签对模型进行训练
# 5.模型评估--->此处不需要

# 6.模型测试
y_test = model.predict(x_test) # 这句话的意思是使用模型对测试集的特征预测对应的标签
print(y_test)

六、KNN在回归任务中的处理方式

1. 同样先计算预测样本与所有训练样本的距离。
2. 找出最近的K个邻居。
3. 将其对应的输出值求取算术平均。
4. 以该平均值作为预测结果。

'''
步骤：
    1- 加载数据
    2- 数据预处理
    3- 特征工程
    4- 模型训练
    5- 模型评估
    6- 模型测试
'''

from sklearn.neighbors import KNeighborsRegressor

# 1.加载数据
x_train = [[0,0,1],[1,1,0],[3,10,10],[4,11,12]] # 训练集的特征
y_train = [0.1,0.2,0.3,0.4]                     # 训练集的标签
x_test = [[3,11,10]]                            # 测试集的特征

# 2.数据预处理--->此处不需要

# 3.特征工程--->此处不需要

# 4.模型训练
'''
主要参数：
n_neighbors=5:K的个数，默认是5。
metric="minkowski":距离公式，默认选择的是闵式距离
p=2:默认是2，当选择2之后，和第二个参数进行合并的话 就是选择的是欧式距离

当距离公式选择的是闵式距离之后，当p=2,代表欧式距离
当距离公式选择的是闵式距离之后，当p=1,代表城市街区距离
当距离公式选择的是闵式距离之后，当p=??,代表切比雪夫距离

欧式距离：对应维度值的差的平方和开平方根（类似与勾股定理）
曼哈顿距离（城市街区距离）：对应维度值的差的绝对值的和
切比雪夫距离：对应维度值的差的最大值
'''
model = KNeighborsRegressor(n_neighbors=2,p=2,metric='minkowski') # 创建KNN回归模型，距离默认是欧式距离
model.fit(x_train,y_train) # 使用训练集的特征和标签对模型进行训练

# 5.模型评估--->此处不需要

# 6.模型测试
y_test = model.predict(x_test) # 使用模型根据测试集的特征预测出测试集样本的标签
print(y_test)

七、超参数的选择策略

KNN的主要超参数包括邻居数量K以及所使用距离的类型。

• K值选择：通常借助交叉验证结合网格搜索（GridSearchCV）来寻找最优K值，避免过拟合或欠拟合。
• 距离度量选择：需根据数据特征分布情况合理选用，例如高维稀疏数据可能更适合曼哈顿距离。

其中，GridSearchCV 是常用的自动化调参工具，能系统地遍历参数组合并评估模型性能。

八、模型性能评估指标

针对不同类型的任务，采用不同的评价标准：

分类任务常用指标：准确率、精确率、召回率、F1分数以及混淆矩阵。

回归任务常用指标：均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）。

九、实战应用示例

通过具体案例可以更好地掌握KNN的实际操作过程：

分类问题演示：

'''
步骤：
    1- 加载数据
    2- 数据预处理
    3- 特征工程
    4- 模型巡礼那
    5- 模型评估
    6- 模型测试
'''
from sklearn.neighbors import KNeighborsClassifier   # KNN分类算法的API
# 1.加载数据
x_train = [[1],[2],[3],[4]] # 训练集的特征
y_train = [0,0,1,1]         # 训练集的标签
x_test = [[5]]              # 测试集的特征

# 2.数据预处理--->此处不需要

# 3.特征工程--->此处不需要

# 4.模型训练
'''
主要参数：
n_neighbors=5:K的个数，默认是5。
metric="minkowski":距离公式，默认选择的是闵式距离
p=2:默认是2，当选择2之后，和第二个参数进行合并的话 就是选择的是欧式距离

当距离公式选择的是闵式距离之后，当p=2,代表欧式距离
当距离公式选择的是闵式距离之后，当p=1,代表曼哈顿距离（城市街区距离）
当距离公式选择的是闵式距离之后，当p=??,代表切比雪夫距离

欧式距离：对应维度值的差的平方和开平方根（类似与勾股定理）
曼哈顿距离（城市街区距离）：对应维度值的差的绝对值的和
切比雪夫距离：对应维度值的差的最大值
'''
# 这句代码只是创建出来了模型，就好像是创建出来汽车外架了，但是发动机什么的都没有
model = KNeighborsClassifier(n_neighbors = 2,metric='minkowski',p=2) # 模型使用的是KNN分类模型，K是2，距离是欧式距离
model.fit(x_train,y_train) # 这句话的意思是使用训练集的特征和标签对模型进行训练
# 5.模型评估--->此处不需要

# 6.模型测试
y_test = model.predict(x_test) # 这句话的意思是使用模型对测试集的特征预测对应的标签
print(y_test)

回归问题演示：

'''
步骤：
    1- 加载数据
    2- 数据预处理
    3- 特征工程
    4- 模型训练
    5- 模型评估
    6- 模型测试
'''

from sklearn.neighbors import KNeighborsRegressor

# 1.加载数据
x_train = [[0,0,1],[1,1,0],[3,10,10],[4,11,12]] # 训练集的特征
y_train = [0.1,0.2,0.3,0.4]                     # 训练集的标签
x_test = [[3,11,10]]                            # 测试集的特征

# 2.数据预处理--->此处不需要

# 3.特征工程--->此处不需要

# 4.模型训练
'''
主要参数：
n_neighbors=5:K的个数，默认是5。
metric="minkowski":距离公式，默认选择的是闵式距离
p=2:默认是2，当选择2之后，和第二个参数进行合并的话 就是选择的是欧式距离

当距离公式选择的是闵式距离之后，当p=2,代表欧式距离
当距离公式选择的是闵式距离之后，当p=1,代表城市街区距离
当距离公式选择的是闵式距离之后，当p=??,代表切比雪夫距离

欧式距离：对应维度值的差的平方和开平方根（类似与勾股定理）
曼哈顿距离（城市街区距离）：对应维度值的差的绝对值的和
切比雪夫距离：对应维度值的差的最大值
'''
model = KNeighborsRegressor(n_neighbors=2,p=2,metric='minkowski') # 创建KNN回归模型，距离默认是欧式距离
model.fit(x_train,y_train) # 使用训练集的特征和标签对模型进行训练

# 5.模型评估--->此处不需要

# 6.模型测试
y_test = model.predict(x_test) # 使用模型根据测试集的特征预测出测试集样本的标签
print(y_test)