1、灰度直方图

灰度直方图是一种用于统计图像中各灰度级别像素数量的图表。通过分析其分布形态，可以快速了解图像的亮度水平、对比度强弱以及曝光是否合理，为后续的图像增强提供参考依据。

一个灰度直方图可能对应多种不同的图像结构，即图像与直方图之间是多对一的关系。即使视觉上差异明显，只要灰度值的分布一致，它们的直方图就相同。

根据直方图的分布特征，可判断图像状态并采取相应处理措施：

• 分布狭窄且集中：说明图像对比度较低（整体偏灰），应进行对比度扩展。
• 集中在左侧（低灰度区）：图像整体偏暗，需提升亮度。
• 集中在右侧（高灰度区）：图像过亮，应降低亮度。

在直方图中，横轴（x轴）表示灰度等级，纵轴（y轴）表示具有该灰度级的像素总数。所有灰度级对应的像素数之和即为直方图的总面积，也等于图像总的像素个数。因此，直方图面积 = 图像总像素数。对该面积沿横轴积分即可得出结果。

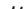
平均灰度反映了图像的整体亮度水平。平均值越高，图像越明亮；反之则越暗。

标准差则体现灰度值的离散程度。标准差越大，说明灰度分布越广，图像的对比度也越高。

需要注意的是，直方图属于全局性统计指标，仅关注某一灰度值出现的频率，而不考虑这些像素在图像中的空间位置。因此，它无法反映物体形状、纹理细节或边缘信息。

尽管不同图像在视觉上可能存在显著差异，但只要它们的灰度值数量分布相同，其直方图就会完全一致。

2、二值化处理

二值化是指将图像中所有像素转换为两个数值，通常为0（黑）和255（白），从而区分前景与背景。实现这一过程需要设定一个阈值T：

• 若像素灰度值 ≥ T，则设为255（白色，前景）；
• 若像素灰度值 < T，则设为0（黑色，背景）。

为了获得最佳分割效果，需选取最优阈值T*，使得前景与背景分离最为清晰准确。为此发展出多种自动选阈算法。

【补充】许多图像的灰度直方图呈现双峰特性：一个峰值位于低灰度区域（对应暗部），另一个位于高灰度区域（对应亮部）。两峰之间的谷底常被视为前景与背景的过渡区域，最优阈值通常取自此谷底位置。

常见的阈值选择方法包括：

（1）全局固定阈值

手动设定阈值，如在8位图像中常用T=128。适用于光照均匀、前景与背景对比明显的场景。

（2）大津法（Otsu）

这是一种经典的自动选取全局阈值的方法。假设图像由前景和背景两类像素构成（即直方图呈双峰分布），通过遍历所有可能的阈值，寻找使类间方差最大（或类内方差最小）的那个灰度值作为最优阈值T。

（3）熵法（Entropy-based Method）

基于信息论原理，通过最大化前景与背景的信息熵来确定最佳分割阈值。

（4）Isodata算法

一种迭代式聚类方法，通过不断调整前景与背景的平均灰度值来逼近最优阈值，属于自适应阈值选择的典型代表之一。

3、直方图均衡化（HE）

直方图均衡化是一种自动增强图像对比度的技术。其核心思想是构建一个映射函数，将原始图像的灰度级重新分布，使得输出图像的直方图尽可能平坦（即均匀分布）。

该方法利用累积分布函数（CDF）对图像进行非线性拉伸，将像素密集的灰度区间展开，稀疏区间压缩，从而有效提升整体对比度。

经过直方图均衡化处理后，图像的灰度分布更加均匀，视觉细节更清晰，同时提高了幅度分辨率。

4、直方图规定化

与均衡化不同，直方图规定化的目标不是让直方图变均匀，而是将其调整为某个预设的目标分布形式。这种方法可以避免因过度拉伸而导致的对比度过强问题。

简而言之，直方图均衡化追求“均匀”，而规定化追求“可控”——使图像直方图匹配特定模板或参考图像的分布。

两者均属于直方图变换技术范畴。为实现从源图像到目标分布的转换，常用两种灰度映射策略：

（1）单映射规则（SML）

采用一对一的直接映射方式，计算简单直观，属于正向映射方法。

（2）组映射规则（GML）

采用多对一映射机制，将输入图像的一段连续灰度范围映射至参考图像的一个灰度级。理论上，GML比SML更优，被认为是更接近理想解的方法。

（3）误差比较

一般情况下，GML的映射误差小于或等于SML。但在某些特殊条件下二者误差相等。具体而言：

• 当原始图像与目标图像的灰度级数相等（M = N）时，SML与GML误差相同；
• 当原始灰度级数大于目标（M > N）时，SML误差必然更大。

图像运算

1、基本几何变换

由于图像像素以坐标（x, y）表示，因此图像变换可视为对这些坐标的数学操作。其中平移是最基础的一种变换形式。

（x'，y'）= ? ( x ± t , y ±? t)

旋转

x' = x·cosθ - y·sinθ；y' = x·sinθ + y·cosθ

缩放

(x', y') = (s_x · x, s_y · y)

翻转

水平镜像：

x' = -x

垂直镜像：

y' = -y

算术与逻辑运算

（1）算术运算（结果通常为灰度值）

• 加法：C(x,y) = A(x,y) + B(x,y)。常用于图像平均以降低噪声，或实现图像融合。
• 减法：C(x,y) = |A(x,y) - B(x,y)|，取绝对值。适用于运动检测、背景消除以及差异分析等场景。
• 乘法/除法：多用于局部增强或校正操作，例如遮罩处理、阴影补偿等。

（2）逻辑运算（通常作用于二值图像或位平面）

• 与（AND）：提取两个图像的共同区域，常用于掩模操作。
• 或（OR）：合并不同区域，形成联合区域。
• 非（NOT）：对像素值进行反转，获取补集。
• 异或（XOR）：识别两幅图像之间的差异部分。

像素间的基本关系与定义

（1）邻域与邻接

4-邻域（N(p)）：指像素 p 的上下左右四个直接相邻的像素点。

对角邻域（N_D(p)）：指像素 p 的四个对角方向上的像素。

8-邻域（N(p)）：包含周围全部八个邻近像素。

N?(p) ∪ N_D(p)

如下图所示：

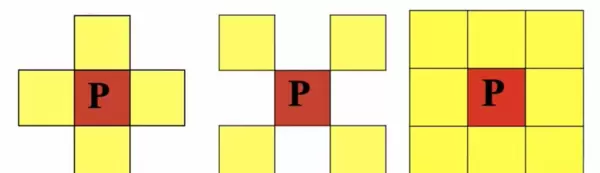
当两个像素在空间上相邻时，可根据特定规则判断其是否构成邻接关系：

• 4-邻接：若像素 q 位于像素 p 的4-邻域内，则二者为4-邻接。
• 8-邻接：若 q 在 p 的8-邻域中，则为8-邻接。
• m-邻接（混合邻接）：为避免8-邻接带来的连接歧义（如通过角点穿越缝隙），引入该概念。满足以下任一条件即为m-邻接：
  1. q 属于 p 的4-邻域；
  2. q 位于 p 的对角位置，且 p 与 q 的4-邻域之间无交集。

关于 m-邻接的进一步说明：需预先定义一个像素值集合 V。例如，在二值图像中设 V = {1}，则所有值为1的像素属于该集合。当两个像素 p 和 q 满足： - 处于4-邻域内，或者 - 处于对角位置，并且它们各自的4-邻域中没有共同属于集合 V 的像素， 则认为 p 和 q 构成 m-邻接。

示例对比：

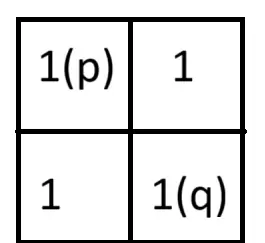
左图中，p 与 q 的4-邻域存在值为1的像素（属于V），因此不满足 m-邻接条件。

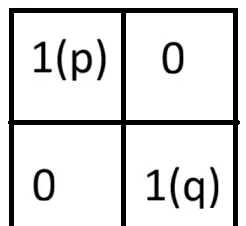
右图中，相应邻域内无属于 V 的像素，故满足 m-邻接。

（2）像素间的距离度量

欧几里得距离（欧式距离）：表示两点之间的直线距离，计算方式为两点坐标差的平方和再开方。

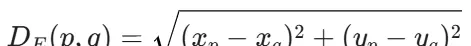
城区距离：仅允许沿水平或垂直方向移动，对应于4-邻接结构。其值等于从点 p 到 q 所需的最小步数（单位步长）。

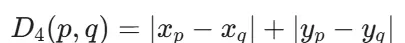
棋盘距离：允许水平、垂直及对角移动，对应8-邻接模式。代表从点 p 到 q 所需的最少移动次数（每步可走一格，包括斜向）。

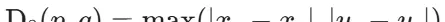
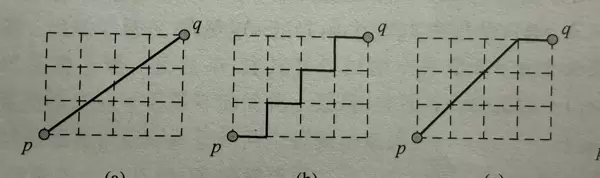
距离示意图如下：

关于模板运算中的卷积与滤波技术，将在后续内容中详细讲解。