在数据可视化中，Matplotlib 提供了多种图表类型以满足不同场景下的分析需求。以下将介绍几种常见的图形绘制方法，包括散点图、饼图、柱状图以及直方图，并展示其基本用法与参数设置。

1、散点图

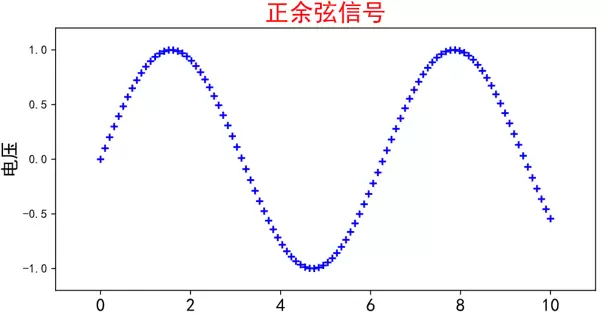
散点图与折线图的主要区别在于：折线图会将各个数据点依次连接，从而形成连续的线条，原始点的位置可能被掩盖；而散点图则直接呈现每个坐标点的独立位置，便于观察数据的整体分布趋势和形态特征。

示例代码如下：

x = np.linspace(0, 10, 100)   # 在0到10之间生成100个均匀分布的数据点
y = np.sin(x)

# 图形配置
plt.figure(figsize=(8, 4), dpi=100)
plt.title('正余弦信号', color='red', fontsize=20, rotation=0, alpha=1)
plt.xlabel('时间', fontsize=15, color='k', rotation=0)
plt.ylabel('电压', fontsize=15)
plt.xlim(-1, 11)
plt.ylim(-1.2, 1.2)
plt.xticks(np.arange(0, 12, 2), fontsize=15, rotation=0)
plt.yticks([-1, -0.5, 0, 0.5, 1])

# 绘制散点图
plt.scatter(x, y, c='blue', s=10, marker='+', label='sin(x)')
    

2、饼图

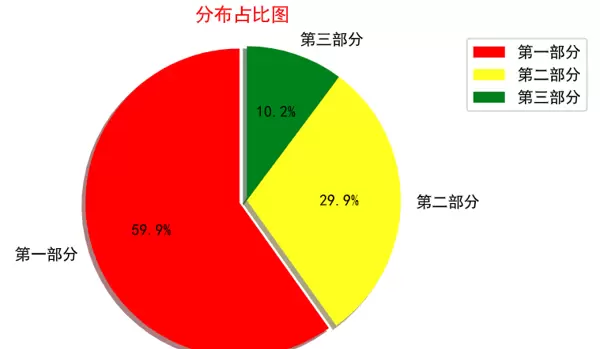
饼图主要用于展示各类别在整体中所占的比例关系，适合用于比例分析。

构建饼图时，需要提供数值列表、标签、颜色等信息，并可通过参数控制显示效果。

# 创建画布
plt.figure(figsize=(8,4))

# 数据定义
values = [63.54, 34.76, 78.46]
labels = ['第一部分', '第二部分', '第三部分']
colors = ['red', 'blue', 'green']

# 设置突出显示的部分（如第一块分离）
explode = (0.15, 0, 0)

# 绘制饼图
plt.pie(values, explode=explode, labels=labels, colors=colors, labeldistance=1.1,
        autopct='%.1f%%', shadow=True, startangle=45, pctdistance=0.6)

# 显示为正圆
plt.axis('equal')
plt.title('分布占比图', color='r')
plt.legend()
    

3、柱状图

柱状图适用于比较分类数据之间的绝对数值大小，相较于饼图更强调数量差异而非比例关系。

基础柱状图示例：

x = np.array([1,2,3,4,5,6])
y = np.array([866, 787, 964, 654, 798, 993])

plt.bar(x, y, width=0.5, label='销售业绩')
plt.legend(loc=0)

# 添加标题
plt.title('上半年每月业绩表现')

# 在柱子上方标注具体数值
for a, b in zip(x, y):
    plt.text(a, b, b, ha='center', va='bottom', fontsize=10)

# 自定义x轴刻度标签
plt.xticks(x, [str(i+1)+'月' for i in range(6)])
plt.show()
    

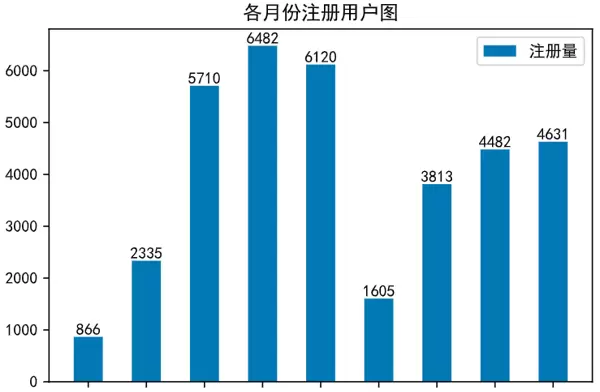
若希望对数据进行排序后再绘图，可利用字典结合排序函数实现：

dic = {'1月': 2001, '2月': 3409, '3月': 2983, '4月': 2001, '5月': 2763, '6月': 2908}

# 按照值从大到小排序，若值相同则按键排序
dic = dict(sorted(dic.items(), key=lambda kv: (kv[1], kv[0]), reverse=True))

# 使用排序后的数据绘图
plt.bar(dic.keys(), dic.values(), width=0.5, label='销售业绩')
    

4、直方图

直方图用于展示连续型数据的分布情况，通过将数据划分为若干区间（即“箱”），统计每个区间内出现的频次，进而反映数据的集中趋势与离散程度。它常用于探索变量的分布形态，例如是否服从正态分布等。

该图表类型在数据分析初期具有重要意义，能帮助快速识别异常值、偏态或双峰现象。

直方图是一种用于展示数据频数分布的统计图表，其外观与柱状图相似，均由一系列矩形条组成。不同之处在于，直方图中的每个矩形面积代表频数或概率密度，其中矩形的宽度表示组距，高度表示频数除以组距。因此，长条的宽度和高度都具有统计意义。当所有组距相等时，通常直接用长条的高度来反映频数大小。

与柱状图相比，两者的应用场景存在明显差异：柱状图适用于展示分类数据之间的比较，而直方图则主要用于呈现连续型数据的分布情况。

下面是一段生成数据并绘制直方图的代码示例：

# 生成数据
data = np.random.randn(1000)    # 生成1000个服从标准正态分布的随机数，均值为0，标准差为1
# bins参数指定将数据范围划分为100个等宽区间
plt.hist(data, bins=100, density=False, facecolor='b', edgecolor='k', alpha=0.7)
plt.xlabel('区间')
plt.ylabel('频次')    # 表示该区间内数据出现的总次数
plt.title('直方图')
plt.show()

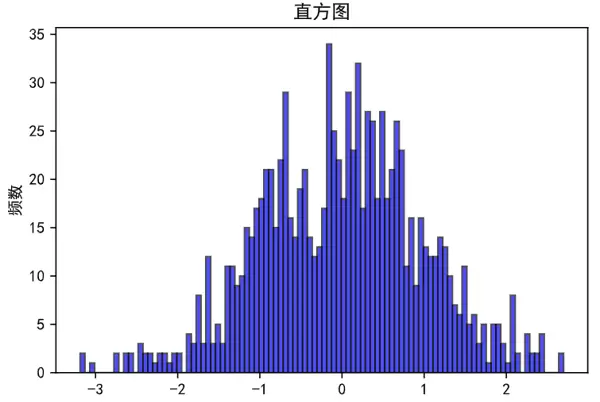
可以尝试将代码中的 density=False 修改为 density=True，观察图形显示结果的变化。此时纵轴将不再表示原始频次，而是表示概率密度值，使得整个直方图下方面的面积总和为1。