技术路线
数据预处理:对原始数据进行随机打乱,并采用归一化方法将输入与输出变量映射至[0,1]区间,提升模型训练稳定性。
模型结构:构建基于RBF(径向基函数)的神经网络模型,核心参数包括中心点、权重以及扩展参数newrbe
。
优化目标:以最小化预测误差为目标,通过智能优化算法搜索最优的RBF扩展参数。目标函数定义为如RMSE等误差指标getObjValue
。
评估体系:引入多种评估指标,包括MAE、RMSE、MAPE和MBE,用于全面衡量模型性能calc_error
。
可视化支持:利用MATLAB内置绘图工具生成适应度曲线、预测结果对比图及误差柱状图等图形化输出数据预处理 → 标准RBF模型 → 智能优化算法 → 优化RBF模型 → 预测评估 → 可视化对比
。
主要功能
- 多算法优化RBF网络:集成多种智能优化算法,自动寻优RBF神经网络中的关键参数
spread
。
- 回归预测能力:支持多输入单输出的连续值预测任务,适用于各类实际工程场景。
- 性能对比分析:系统性比较不同优化策略在训练集与测试集上的表现,输出适应度演化过程、预测效果对比以及误差指标对比图
 。
。
算法实现步骤
- 数据准备:读取Excel格式的数据文件(默认7个输入特征,1个输出标签),按7:3比例随机划分训练集与测试集。
- 数据归一化:使用最大-最小标准化方法,将所有特征和目标变量统一缩放到[0,1]范围内
mapminmax
。
- 基准模型构建:建立标准RBF网络作为对照组,采用固定初始扩展参数进行建模
spread=100
。
- 智能优化循环:
- 从指定文件夹加载各优化算法脚本
spread
,对RBF的扩展参数进行迭代优化。
- 将优化所得的最佳
spread
代入RBF网络重新训练。
- 计算并保存对应模型在训练集和测试集上的预测性能指标。
- 结果可视化:
- 绘制各算法在优化过程中的适应度收敛曲线。
- 展示训练集与测试集中真实值与预测值的对比图表。
- 生成包含MAE、RMSE、MAPE、MBE四项指标的柱状图以便横向比较
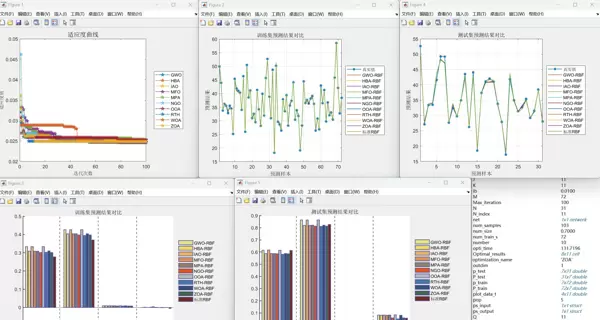 。
。
公式原理说明
RBF神经网络的输出表达式如下:
\( \hat{y} = \sum_{i=1}^{m} w_i \cdot \phi(||x - c_i||) \)
其中:
- \( \phi \) 表示径向基函数,通常选用高斯核函数;
- \( c_i \) 为第 \( i \) 个隐含层节点的中心向量;
- \( w_i \) 是对应的线性组合权重;
- 扩展参数(spread)控制基函数的覆盖宽度,直接影响模型泛化能力
spread
。
优化目标函数定义为:
\( f(\text{spread}) = \text{预测误差指标(例如RMSE)} \)
优化算法通过不断调整spread
,寻找使该目标函数最小化的最优参数配置getObjValue
。
参数设置说明
| 参数名称 |
描述 |
默认值 |
num_size
训练集占比 |
用于划分训练与测试数据的比例 |
0.7 |
rbf_spread
RBF扩展参数(初始值) |
标准RBF模型中使用的初始spread值 |
100 |
lb
, ub
优化边界 |
智能算法搜索范围的上下限 |
[0.01, 1000] |
pop
种群规模 |
每代参与进化的个体数量 |
5 |
Max_iteration
最大迭代次数 |
算法终止条件之一 |
100 |
N_index
算法总数(含标准RBF) |
参与对比的算法数量 |
11 |
运行环境要求
- 软件平台:MATLAB R2018a 或更高版本。
- 依赖组件:
- 所有智能优化算法实现代码需存放于指定目录
可优化RBF的智能优化算法/
;
- 必需函数文件:
calc_error.m
和 getObjValue.m
;
- 绘图配色方案依赖外部颜色配置文件
科研绘画桶.mat
。
- 数据格式要求:输入数据应为Excel文件,包含7个输入变量和1个输出变量。
典型应用场景
本模型框架适用于各类需要高精度回归预测的实际问题,例如:
- 房价趋势预测
- 股票价格走势建模
- 电力系统负荷估计
- 商品销量预测
- 风速时间序列预测
- 环境监测数据预测(如水质、空气质量)
总结
该MATLAB程序实现了一个通用的多算法对比优化框架,专注于利用多种智能优化算法对RBF神经网络的关键扩展参数进行自动调参。通过系统比较不同算法在相同任务下的性能表现,可用于科研探索或工程实践中对预测模型的精细化优化需求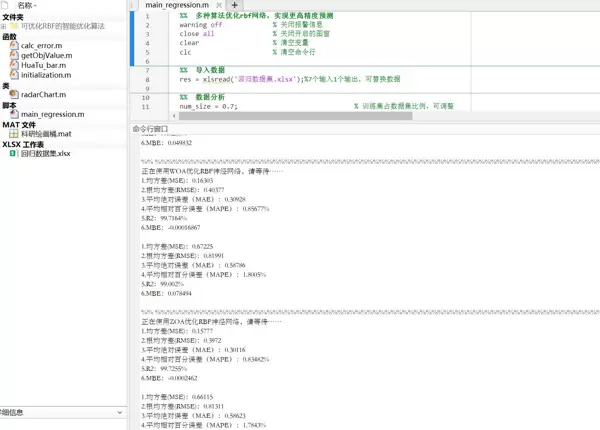 。
。

 扫码加好友,拉您进群
扫码加好友,拉您进群