分数布朗运动(FBM)及其在金融中的应用文献12篇
本帖隐藏的内容
汇总
 Fractional Brownian Motion Modelling in Finance(12papers).zip
大小:(2.01 MB)
Fractional Brownian Motion Modelling in Finance(12papers).zip
大小:(2.01 MB)
马上下载
本附件包括:
- 12 fractional_Brownian_motion based on Wavelets.pdf
- 1 Fractional Brownian Motion and applications to fnancial Modelling.pdf
- 2 Parameter estimation of geometrically sampled fractionalBrownian traffic.pdf
- 3 Arbitrage in fractional Brownian motion.pdf
- 4 Inherent_Exclusion_of_Arbitrage FBM.pdf
- 5 Fractional Brownian motion stochastic calculus.pdf
- 6 Option_Pricing_in_a_Fractional_Brownian_Motion.pdf
- 7 A_random_walk_approximation_to_fractional_Brownian_motion.pdf
- 8 FRACTIONAL BROWNIAN MOTION theory and application.pdf
- 9 FBM in Finance.pdf
- 10 Stochastic Differential Equations Driven by FBM and SBM.pdf
- 11 Fractional Brownian motion Simulation Code and Method.pdf



A normalized fractional Brownian motion (fBm), also called a fractal Brownian motion, is a generalization of Brownian motion without independent increments. It is a continuous-time Gaussian process BH(t) on [0, T], which starts at zero, has expectation zero for all t in [0, T], and has the following covariance function:
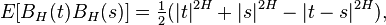 .
.
where H is a real number in (0, 1), called the Hurst index or Hurst parameter associated with the fractional Brownian motion. The Hurst exponent describes the raggedness of the resultant motion, with a higher value leading to a smoother motion. It was introduced by Mandelbrot & van Ness (1968).
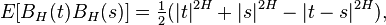
The value of H determines what kind of process the fBm is:if H = 1/2 then the process is in fact a Brownian motion or Wiener process;if H > 1/2 then the increments of the process are positively correlated;if H < 1/2 then the increments of the process are negatively correlated.The increment process, X(t) = BH(t+1) − BH(t), is known as fractional Gaussian noise.
Prior to the introduction of the fractional Brownian motion,Lévy (1953) used the Riemann–Liouville fractional integral to define the process:

where integration is with respect to the white noise measure dB(s). This integral turns out to be ill-suited to applications of fractional Brownian motion.
The idea instead is to use a different fractional integral of white noise to define the process: the Weyl integral
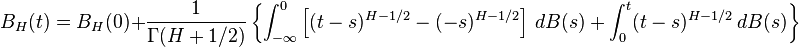
The main difference between fractional Brownian motion and regular Brownian motion is that while the increments in Brownian Motion are independent.

 扫码加好友,拉您进群
扫码加好友,拉您进群