生产多少可乐到达利益最大化？

既然可以共存赚钱，那如何确定最优产量以使自己达到利益最大化呢？首先，对于消费者来说，可乐价格越贵，购买量就会越少。因此可以简单地认为价格 p 和可乐总需求 q 呈反比关系（用 p = a - b×q 表示）。为方便起见，我们设市场上只有可口可乐（产量 q 1 ）和百事可乐（产量 q 2 ）两家可乐公司，且他们的产量之和等于消费者对可乐的需求，也就是 q = q 1 + q 2 。假设对于两家公司每罐可乐的成本一样，均为 c，那对于可口可乐来说，其盈利为

对 q 1 求导并令其等于 0 即可得到使得可口可乐盈利最大时的产量 q 1 ^= (a - c) / 2b - q2 / 2。同理能算出百事可乐的最佳产量 q 2 ^ = (a - c) / 2b - q 1 / 2。

我们建立一个直角坐标系，横坐标为 q 1 ，纵坐标 q 2 ，然后把两个商家的最优产量随另一个商家产量的变化关系画在一起，得到下面的图。图中标出 Q 1 、 Q 2 分别为可口可乐和百事可乐的最优产量曲线。在 Q 1 上，对给定的 q 2 ，可以把 Q 1 上的点的横坐标即为可口可乐的最优产量 q 1 ^，而 Q 2 表示给定一个 q 1 ，其对应 Q 2 上的点的纵坐标则是百事可乐的最优产量 q 2 ^。

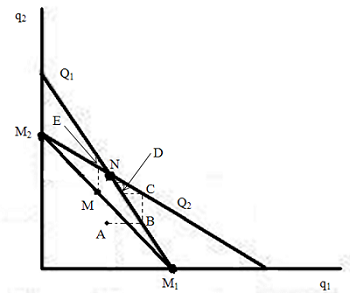
那两家公司的产量策略会对应于图上的哪一点呢？那就是两条最佳策略线的交点 N，因为这里表示双方同时达到最佳策略。假设一开始两家的策略对应于图上任意一点，比如 A，如果可口可乐最先意识到将策略按最佳策略线 Q 1 调整时自己获利最大，它就会立刻改变产量，策略从点 A 移动到 B，这时，百事可乐自然知道需要把策略移到自己的最佳策略线 Q2 上，因此策略从 B 移到 C。为了让策略回到 Q 1 上，可口可乐选择降低自己的产量，策略又从 C 移动到 D。从图上可以看见，由于双方都希望策略位于自己的最佳策略线，最后的结果是策略趋向于 Q 1 和 Q 2 的交点 N。

而图中的 M 1 表示可口可乐垄断市场，百事可乐一点都不生产。根据经济学的一点知识，完全垄断是所有市场形式中利润最高的。类似的， M 2 表示百事可乐完全垄断。那么， M1 和 M 2 的中点 M 表示是什么呢？这就好比把可口可乐和百事合并成一个公司，实施垄断经营，然后把利润平分。这样每个公司得到的利润是最大的，高于 N 点。然而，要说服大家离开N而合作到达 M 是很困难的。一方面，如果一家不讲信用，就可以通过设置自己的产量获得更大的利润，而对手则蒙受损失。另外，两家保持垄断会吸引新的厂商进入市场，从而导致垄断破裂。

然而，脱离 N 点也并非不可能，至少百事和可口可乐就做到了。一方面，两家公司其实一直在重复这个博弈，这使得脱离纳什均衡选择收益更大的策略更有可能。如果一方违反默契，可能造成对方的报复，进而损失更多的利益。另外，可乐生产尽管不是什么高科技，但大家早就对这两家公司有了品牌认同感，新的公司想要抢占市场还是很困难的。

呵呵 果然是学者，促销能用囚徒困境解释的如此专业！

分析的很有道理，不知道实际操作如何？百事和可口促销是否追从此类博弈结果

我也进来看看哈                                                                        
                                       
                                                     
                                                     
                                             
                                                                 
                                                                                 

楼主好像是博弈学方面研究的哦，谢谢分享