Clarification on analytic weights with linear regression

A popular request on the help line is to describe the effect of specifying [aweight=exp] with regress in terms of transformation of the dependent and independent variables. The mechanical answer is that typing

        . regress y x_1 x_2 [aweight=n]

is equivalent to estimating the model:

This regression will reproduce the coefficients and covariance matrix produced by the aweighted regression. The mean square errors (estimate of the variance of the residuals) will, however, be different. The transformed regression reports 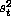, an estimate of Var(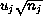). Theaweighted regression reports , an estimate of Var(), where N is the number of observations. Thus,

The logic for this adjustment is as follows: Consider the model:

Assume that, were this model estimated on individuals, Var(u)=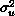, a constant. Assume that individual data are not available; what is available are averages , for j = 1,...,N, and that each average is calculated over observations. Then it is still true that

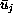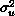where is the average of mean 0, variance deviates, and so has variance . Thus, multiplying through by 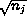produces

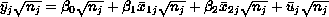
and Var(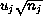)=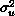. The mean square error 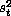reported by estimating this transformed regression is an estimate of 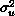. Alternatively, the coefficients and covariance matrix could be obtained by aweighted regress. The only difference would be in the reported mean square error, which per equation 1 is . On average, each observation in the data reflects the averages calculated over 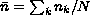individuals, and thus this reported mean square error is the average variance of an observation in the dataset. One can retrieve the estimate of 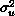by multiplying the reported mean square error by .

More generally, aweights are used to solve general heteroskedasticity problems. In these cases, one has the model

and the variance of is thought to be proportional to . If the variance is proportional to , it is also proportional to , where is any positive constant. Not quite arbitrarily, but with no loss of generality, let us choose , the average value of the inverse of . We can then write Var() = , where k is the constant of proportionality that is no longer a function of the scale of the weights.

Dividing this regression through by the ,

produces a model with Var(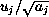) = 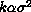, which is the constant part of Var(). Notice in particular that this variance is a function of , the average of the reciprocal weights. If the weights are scaled arbitrarily, then so is this variance.

We can also estimate this model by typing:

        . regress y x_1 x_2 [aweight=1/a]

This command will produce the same estimates of the coefficients and covariance matrix; the reported mean square error is, per equation 1,. This variance is independent of the scale of .