经管之家App
让优质教育人人可得
立即打开
part1—-面试常见内容及面试技巧
机器学习、大数据相关岗位的职责
自己参与面试的提供算法岗位的公司有 BAT、小米、360、飞维美地、宜信、猿题库 等，根据业务的不同，岗位职责大概分为：
平台搭建类
数据计算平台搭建，基础算法实现，当然，要求支持大样本量、高维度数据，所以可能还需要底层开发、并行计算、分布式计算等方面的知识；
算法研究类
1.文本挖掘，如领域知识图谱构建、垃圾短信过滤等；
2.推荐，广告推荐、APP 推荐、题目推荐、新闻推荐等；
3.排序，搜索结果排序、广告排序等；
4.广告投放效果分析；
5.互联网信用评价；
6图像识别、理解。
数据挖掘类
商业智能，如统计报表；
用户体验分析，预测流失用户。
以上是根据本人求职季有限的接触所做的总结。有的应用方向比较成熟，业界有足够的技术积累，比如搜索、推荐，也有的方向还有很多开放性问题等待探索，比如互联网金融、互联网教育。在面试的过程中，一方面要尽力向企业展现自己的能力，另一方面也是在增进对行业发展现状与未来趋势的理解，特别是可以从一些刚起步的企业和团队那里，了解到一些有价值的一手问题。
以下首先介绍面试中遇到的一些真实问题，然后谈一谈答题和面试准备上的建议。
面试问题
你在研究/项目/实习经历中主要用过哪些机器学习/数据挖掘的算法？
你熟悉的机器学习/数据挖掘算法主要有哪些？
你用过哪些机器学习/数据挖掘工具或框架？
基础知识
无监督和有监督算法的区别？
SVM 的推导，特性？多分类怎么处理？
LR 的推导，特性？
决策树的特性？
SVM、LR、决策树的对比？
GBDT 和 决策森林 的区别？
如何判断函数凸或非凸？
解释对偶的概念。
如何进行特征选择？
为什么会产生过拟合，有哪些方法可以预防或克服过拟合？
介绍卷积神经网络，和 DBN 有什么区别？
采用 EM 算法求解的模型有哪些，为什么不用牛顿法或梯度下降法？
用 EM 算法推导解释 Kmeans。
用过哪些聚类算法，解释密度聚类算法。
聚类算法中的距离度量有哪些？
如何进行实体识别？
解释贝叶斯公式和朴素贝叶斯分类。
写一个 Hadoop 版本的 wordcount。
……
开放问题
给你公司内部群组的聊天记录，怎样区分出主管和员工？
如何评估网站内容的真实性（针对代刷、作弊类）？
深度学习在推荐系统上可能有怎样的发挥？
路段平均车速反映了路况，在道路上布控采集车辆速度，如何对路况做出合理估计？采集数据中的异常值如何处理？
如何根据语料计算两个词词义的相似度？
在百度贴吧里发布 APP 广告，问推荐策略？
如何判断自己实现的 LR、Kmeans 算法是否正确？
100亿数字，怎么统计前100大的？
……
答题思路
用过什么算法？
最好是在项目/实习的大数据场景里用过，比如推荐里用过 CF、LR，分类里用过 SVM、GBDT；
一般用法是什么，是不是自己实现的，有什么比较知名的实现，使用过程中踩过哪些坑；
优缺点分析。
熟悉的算法有哪些？
基础算法要多说，其它算法要挑熟悉程度高的说，不光列举算法，也适当说说应用场合；
面试官和你的研究方向可能不匹配，不过在基础算法上你们还是有很多共同语言的，你说得太高大上可能效果并不好，一方面面试官还是要问基础的，另一方面一旦面试官突发奇想让你给他讲解高大上的内容，而你只是泛泛的了解，那就傻叉了。
用过哪些框架/算法包？
主流的分布式框架如 Hadoop，Spark，Graphlab，Parameter Server 等择一或多使用了解；
通用算法包，如 mahout，scikit，weka 等；
专用算法包，如 opencv，theano，torch7，ICTCLAS 等。
基础知识
对知识进行结构化整理，比如撰写自己的 cheet sheet，我觉得面试是在有限时间内向面试官输出自己知识的过程，如果仅仅是在面试现场才开始调动知识、组织表达，总还是不如系统的梳理准备；
从面试官的角度多问自己一些问题，通过查找资料总结出全面的解答，比如如何预防或克服过拟合。
产生背景，适用场合（数据规模，特征维度，是否有 Online 算法，离散/连续特征处理等角度）；
原理推导（最大间隔，软间隔，对偶）；
求解方法（随机梯度下降、拟牛顿法等优化算法）；
优缺点，相关改进；
和其他基本方法的对比；
个人感觉高频话题是 SVM、LR、决策树（决策森林）和聚类算法，要重点准备；
算法要从以下几个方面来掌握:
产生背景，适用场合（数据规模，特征维度，是否有 Online 算法，离散/连续特征处理等角度）；
原理推导（最大间隔，软间隔，对偶）；
求解方法（随机梯度下降、拟牛顿法等优化算法）；
优缺点，相关改进；
和其他基本方法的对比；
不能停留在能看懂的程度，还要:
对知识进行结构化整理，比如撰写自己的 cheet sheet，我觉得面试是在有限时间内向面试官输出自己知识的过程，如果仅仅是在面试现场才开始调动知识、组织表达，总还是不如系统的梳理准备；
从面试官的角度多问自己一些问题，通过查找资料总结出全面的解答，比如如何预防或克服过拟合。
开放问题
由于问题具有综合性和开放性，所以不仅仅考察对算法的了解，还需要足够的实战经验作基础；
先不要考虑完善性或可实现性，调动你的一切知识储备和经验储备去设计，有多少说多少，想到什么说什么，方案都是在你和面试官讨论的过程里逐步完善的，不过面试官有两种风格：引导你思考考虑不周之处 or 指责你没有考虑到某些情况，遇到后者的话还请注意灵活调整答题策略;
和同学朋友开展讨论，可以从上一节列出的问题开始。
准备建议
基础算法复习两条线
1.材料阅读 包括经典教材（比如 PRML，模式分类）、网上系列博客，系统梳理基础算法知识；
2.面试反馈 面试过程中会让你发现自己的薄弱环节和知识盲区，把这些问题记录下来，在下一次面试前搞懂搞透。
除算法知识，还应适当掌握一些系统架构方面的知识，可以从网上分享的阿里、京东、新浪微博等的架构介绍 PPT 入手，也可以从 Hadoop、Spark 等的设计实现切入。
如果真的是以就业为导向就要在平时注意实战经验的积累，在科研项目、实习、比赛（Kaggle，阿里大数据竞赛等）中摸清算法特性、熟悉相关工具与模块的使用。
总结
如今，好多机器学习、数据挖掘的知识都逐渐成为常识，要想在竞争中脱颖而出，就必须做到
1.保持学习热情，关心热点；
2.深入学习，会用，也要理解；
3.在实战中历练总结；
4.积极参加学术界、业界的讲座分享，向牛人学习，与他人讨论。
作者：@太极儒
原文链接
part2—笔试题及答案
2013百度校园招聘数据挖掘工程师
一、简答题（30分）
1、简述数据库操作的步骤（10分）
步骤：建立数据库连接、打开数据库连接、建立数据库命令、运行数据库命令、保存数据库命令、关闭数据库连接。
经萍萍提醒，了解到应该把preparedStatement预处理也考虑在数据库的操作步骤中。此外，对实时性要求不强时，可以使用数据库缓存。
2、TCP/IP的四层结构（10分）
3、什么是MVC结构，简要介绍各层结构的作用（10分）
Model、view、control。
我之前有写过一篇《MVC层次的划分》
二、算法与程序设计（45分）
1、由a-z、0-9组成3位的字符密码，设计一个算法，列出并打印所有可能的密码组合（可用伪代码、C、C++、Java实现）（15分）
把a-z,0-9共（26+10）个字符做成一个数组，然后用三个for循环遍历即可。每一层的遍历都是从数组的第0位开始。
2、实现字符串反转函数（15分）（可用伪代码、C、C++、Java实现）
C++
3、百度凤巢系统，广告客户购买一系列关键词，数据结构如下：（15分）
User1 手机 智能手机 iphone 台式机 …
User2 手机 iphone 笔记本电脑 三星手机 …
User3 htc 平板电脑 手机 …
（1）根据以上数据结构对关键词进行KMeans聚类，请列出关键词的向量表示、距离公式和KMeans算法的整体步骤
KMeans方法一个很重要的部分就是如何定义距离，而距离又牵扯到特征向量的定义，毕竟距离是对两个特征向量进行衡量。
本题中，我们建立一个table。
只要两个关键词在同一个user的描述中出现，我们就将它在相应的表格的位置加1.
这样我们就有了每个关键词的特征向量。
例如：
<手机>=（1,1,2,1,1,1,0,0）
<智能手机> = （1,1,1,1,0,0,0,0）
我们使用夹角余弦公式来计算这两个向量的距离。
夹角余弦公式：
设有两个向量a和b，
，
所以，cos<手机，智能机>=（1+1+2+1）/(sqrt(7+2^2)*sqrt(4))=0.75
cos<手机，iphone>=(2+1+2+1+1+1)/(sqrt(7+2^2)*sqrt(2^2+5))=0.80
夹角余弦值越大说明两者之间的夹角越小，夹角越小说明相关度越高。
通过夹角余弦值我们可以计算出每两个关键词之间的距离。
特征向量和距离计算公式的选择（还有其他很多种距离计算方式，各有其适应的应用场所）完成后，就可以进入KMeans算法。
KMeans算法有两个主要步骤：1、确定k个中心点；2、计算各个点与中心点的距离，然后贴上类标，然后针对各个类，重新计算其中心点的位置。
初始化时，可以设定k个中心点的位置为随机值，也可以全赋值为0。
KMeans的实现代码有很多，这里就不写了。
不过值得一提的是MapReduce模型并不适合计算KMeans这类递归型的算法，MR最拿手的还是流水型的算法。KMeans可以使用MPI模型很方便的计算（庆幸的是YARN中似乎开始支持MPI模型了），所以hadoop上现在也可以方便的写高效算法了（但是要是MRv2哦）。
（2）计算给定关键词与客户关键词的文字相关性，请列出关键词与客户的表达符号和计算公式
这边的文字相关性不知道是不是指非语义的相关性，而只是词频统计上的相关性？如果是语义相关的，可能还需要引入topic model来做辅助（可以看一下百度搜索研发部官方博客的这篇【语义主题计算】）……
如果是指词频统计的话，个人认为可以使用Jaccard系数来计算。
通过第一问中的表格，我们可以知道某个关键词的向量，现在将这个向量做一个简单的变化：如果某个分量不为0则记为1，表示包含这个分量元素，这样某个关键词就可以变成一些词语的集合，记为A。
客户输入的关键词列表也可以表示为一个集合，记为B
Jaccard系数的计算方法是：
所以，假设某个用户userX的关键词表达为：{三星手机，手机，平板电脑}
那么，关键词“手机”与userX的关键词之间的相关性为：
J(“手机”，“userX关键词”)=|{三星手机，手机，平板电脑}|/|{手机，智能手机，iphone，台式机，笔记本电脑，三星手机，HTC，平板电脑}| = 3/8
关键词“三星手机”与用户userX的关键词之间的相关性为：
J(“三星手机”，“userX关键词”)=|{手机，三星手机}|/|{手机，三星手机，iphone，笔记本电脑，平板电脑}| = 2/5
三、系统设计题（25分）
一维数据的拟合，给定数据集{xi,yi}(i=1,…,n)，xi是训练数据，yi是对应的预期值。拟使用线性、二次、高次等函数进行拟合
线性：f(x)=ax+b
二次：f(x)=ax^2+bx+c
三次：f(x)=ax^3+bx^2+cx+d
（1）请依次列出线性、二次、三次拟合的误差函数表达式（2分）
误差函数的计算公式为：
系数1/2只是为了之后求导的时候方便约掉而已。
那分别将线性、二次、三次函数带入至公式中f(xi)的位置，就可以得到它们的误差函数表达式了 。
（2）按照梯度下降法进行拟合，请给出具体的推导过程。（7分）
假设我们样本集的大小为m，每个样本的特征向量为X1=(x11,x12, …, x1n)。
那么整个样本集可以表示为一个矩阵：
其中每一行为一个样本向量。
我们假设系数为θ，则有系数向量：
对于第 i 个样本，我们定义误差变量为
我们可以计算cost function：
由于θ是一个n维向量，所以对每一个分量求偏导：
梯度下降的精华就在于下面这个式子：
这个式子是什么意思呢？是将系数减去导数（导数前的系数先暂时不用理会），为什么是减去导数？我们看一个二维的例子。
假设有一个曲线如图所示：
假设我们处在红色的点上，那么得到的导数是个负值。此时，我在当前位置（x轴）的基础上减去一个负值，就相当于加上了一个正值，那么就朝导数为0的位置移动了一些。
如果当前所处的位置是在最低点的右边，那么就是减去一个正值（导数为正），相当于往左移动了一些距离，也是朝着导数为0的位置移动了一些。
这就是梯度下降最本质的思想。
那么到底一次该移动多少呢？就是又导数前面的系数α来决定的。
现在我们再来看梯度下降的式子，如果写成矩阵计算的形式（使用隐式循环来实现），那么就有：
这边会有点棘手，因为j确定时，xij为一个数值（即，样本的第j个分量），Xθ-Y为一个m*1维的列向量（暂时称作“误差向量”）。
括号里面的部分就相当于：
第1个样本第j个分量*误差向量 + 第2个样本第j个分量*误差向量 + … + 第m个样本第j个分量*误差向量
我们来考察一下式子中各个部分的矩阵形式。
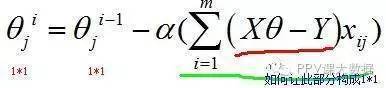
当j固定时，相当于对样本空间做了一个纵向切片，即：
那么此时的xij就是m*1向量，所以为了得到1*1的形式，我们需要拼凑 (1*m)*(m*1)的矩阵运算，因此有：
如果把θ向量的每个分量统一考虑，则有：
关于θ向量的不断更新的终止条件，一般以误差范围（如95%）或者迭代次数（如5000次）进行设定。
梯度下降的有点是：
不像矩阵解法那么需要空间（因为矩阵解法需要求矩阵的逆）
缺点是：如果遇上非凸函数，可能会陷入局部最优解中。对于这种情况，可以尝试几次随机的初始θ，看最后convergence时，得到的向量是否是相似的。
（3）下图给出了线性、二次和七次拟合的效果图。请说明进行数据拟合时，需要考虑哪些问题。在本例中，你选择哪种拟合函数。（8分）
因为是在网上找的题目，没有看到图片是长什么样。大致可能有如下几种情况。
如果是如上三幅图的话，当然是选择中间的模型。
欠拟合的发生一般是因为假设的模型过于简单。而过拟合的原因则是模型过于复杂且训练数据量太少。
对于欠拟合，可以增加模型的复杂性，例如引入更多的特征向量，或者高次方模型。
对于过拟合，可以增加训练的数据，又或者增加一个L2 penalty，用以约束变量的系数以实现降低模型复杂度的目的。
L2 penalty就是：
（注意不要把常数项系数也包括进来，这里假设常数项是θ0）
另外常见的penalty还有L1型的：
（L1型的主要是做稀疏化，即sparsity）
两者为什么会有这样作用上的区别可以找一下【统计之都】上的相关文章看一下。我也还没弄懂底层的原因是什么。
（4）给出实验方案（8分）
2013网易实习生招聘 岗位：数据挖掘工程师
一、问答题
a) 欠拟合和过拟合的原因分别有哪些？如何避免？
欠拟合：模型过于简单；过拟合：模型过于复杂，且训练数据太少。
b) 决策树的父节点和子节点的熵的大小？请解释原因。
父节点的熵>子节点的熵
c) 衡量分类算法的准确率，召回率，F1值。
d) 举例序列模式挖掘算法有哪些？以及他们的应用场景。
DTW（动态事件规整算法）：语音识别领域，判断两端序列是否是同一个单词。
Holt-Winters（三次指数平滑法）：对时间序列进行预测。时间序列的趋势、季节性。
Apriori
Generalized Sequential Pattern(广义序贯模式)
PrefixSpan
二、计算题
1) 给你一组向量a，b
a) 计算二者欧氏距离
(a-b)(a-b)T
即：
b) 计算二者曼哈顿距离
2) 给你一组向量a，b，c，d
a) 计算a，b的Jaccard相似系数
b) 计算c，d的向量空间余弦相似度
c) 计算c、d的皮尔森相关系数
即线性相关系数。
或者
三、（题目记得不是很清楚）
一个文档-词矩阵，给你一个变换公式tfij’=tfij*log(m/dfi)；其中tfij代表单词i在文档f中的频率，m代表文档数，dfi含有单词i的文档频率。
1) 只有一个单词只存在文档中，转换的结果？（具体问题忘记）
2) 有多个单词存在在多个文档中，转换的结果？（具体问题忘记）
3) 公式变换的目的？
四、推导朴素贝叶斯分类P(c|d)，文档d（由若干word组成），求该文档属于类别c的概率，
并说明公式中哪些概率可以利用训练集计算得到。
五、给你五张人脸图片。
可以抽取哪些特征？按照列出的特征，写出第一个和最后一个用户的特征向量。
六、考查ID3算法，根据天气分类outlook/temperature/humidity/windy。（给你一张离散型
的图表数据，一般学过ID3的应该都知道）
a) 哪一个属性作为第一个分类属性？
b) 画出二层决策树。
七、购物篮事物（关联规则）
一个表格：事物ID/购买项。
1) 提取出关联规则的最大数量是多少？（包括0支持度的规则）
2) 提取的频繁项集的最大长度（最小支持>0）
3) 找出能提取出4-项集的最大数量表达式
4) 找出一个具有最大支持度的项集（长度为2或更大）
5) 找出一对项a，b，使得{a}->{b}和{b}->{a}有相同置信度。
八、一个发布优惠劵的网站，如何给用户做出合适的推荐？有哪些方法？设计一个合适的系
统（线下数据处理，存放，线上如何查询？）
扫码加好友，拉您进群
全部版块
我的主页
收藏
