1# 0511010145

假设x(p,w)满足弱公理，则有：

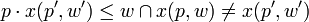
if then

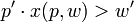
设 p = p0,w = w0,p' = αp0,w' = αw0,直接代入弱公理，我们有：

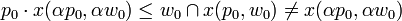
if then

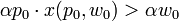
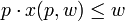
这个then后面的推论显然是不成立的，因为对于任何的p,w我们必须有。因此，if 部分也必然不成立，我们因此有if部分的否命题成立：



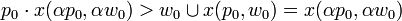
到这一步我们还是没法推论x(p0,w0) = x(αp0,αw0)，因为有前面那个“或”的命题。 现在考虑“或”前面的那个命题。这个命题也是不可能成立的，因为如果在不等式两边同时乘α，我们就有：


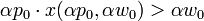
跟then 命题必然不成立的道理一样。“或”前面的命题必然不成立，而整个命题成立，那么我们就必然有

x(p0,w0) = x(αp0,αw0)

成立了。x(p,w)零阶齐次证毕.

2# twomantou
非常谢谢