自本系列第一讲推出以来，得到了不少同学的反响和赞成，也有同学留言说最好能把数学推导部分写的详细点，笔者只能说尽力，因为打公式实在是太浪费时间了。。本节要和大家一起学习的是逻辑（logistic）回归模型，继续按照手推公式+纯 Python 的写作套路。

逻辑回归本质上跟逻辑这个词不是很搭边，叫这个名字完全是直译过来形成的。那该怎么叫呢？其实逻辑回归本名应该叫对数几率回归，是线性回归的一种推广，所以我们在统计学上也称之为广义线性模型。众多周知的是，线性回归针对的是标签为连续值的机器学习任务，那如果我们想用线性模型来做分类任何可行吗？答案当然是肯定的。

sigmoid 函数

相较于线性回归的因变量 y 为连续值，逻辑回归的因变量则是一个 0/1 的二分类值，这就需要我们建立一种映射将原先的实值转化为 0/1 值。这时候就要请出我们熟悉的 sigmoid 函数了：

其函数图形如下：

除了长的很优雅之外，sigmoid 函数还有一个很好的特性就是其求导计算等于下式，这给我们后续求交叉熵损失的梯度时提供了很大便利。

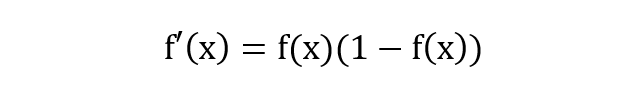
逻辑回归模型的数学推导

由 sigmoid 函数可知逻辑回归模型的基本形式为：

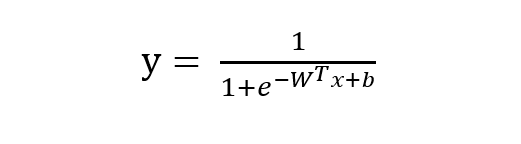
稍微对上式做一下转换：

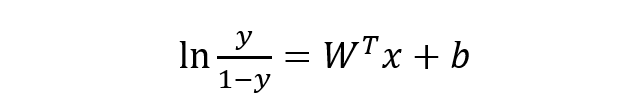
下面将 y 视为类后验概率 p(y = 1 | x)，则上式可以写为：

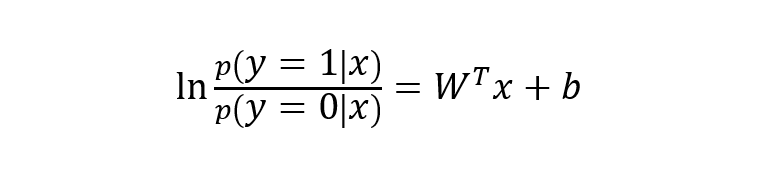
则有：

    将上式进行简单综合，可写成如下形式：

写成对数形式就是我们熟知的交叉熵损失函数了，这也是交叉熵损失的推导由来：

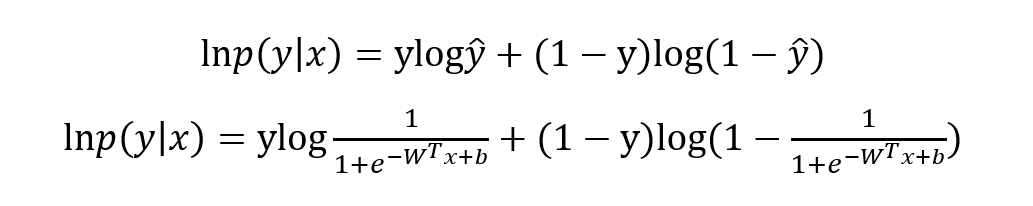
最优化上式子本质上就是我们统计上所说的求其极大似然估计，可基于上式分别关于 W 和b 求其偏导可得：

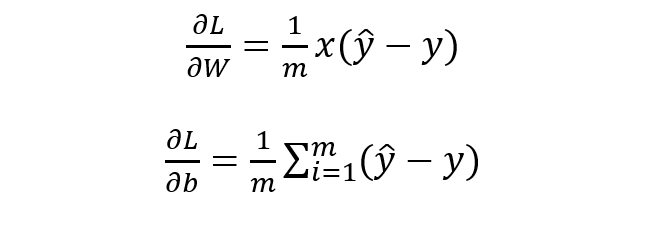
基于 W 和 b 的梯度进行权值更新即可求导参数的最优值，使得损失函数最小化，也即求得参数的极大似然估计，殊途同归啊。

逻辑回归的 Python 实现

跟上一讲写线性模型一样，在实际动手写之前我们需要理清楚思路。要写一个完整的逻辑回归模型我们需要：sigmoid函数、模型主体、参数初始化、基于梯度下降的参数更新训练、数据测试与可视化展示。

先定义一个 sigmoid 函数：

定义模型参数初始化函数：

定义逻辑回归模型主体部分，包括模型计算公式、损失函数和参数的梯度公式：

定义基于梯度下降的参数更新训练过程：

定义对测试数据的预测函数：

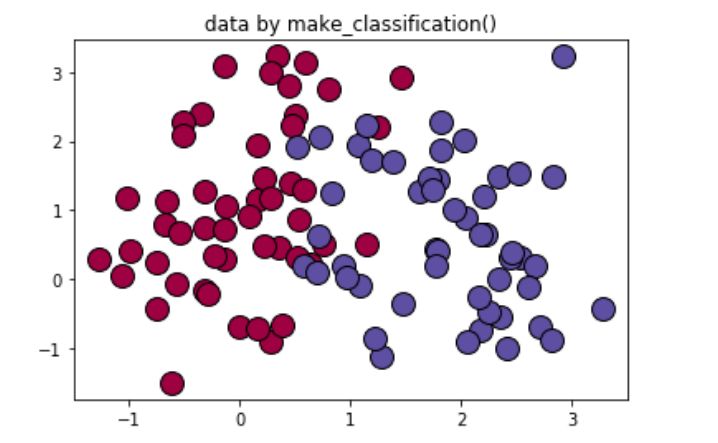
使用 sklearn 生成模拟的二分类数据集进行模型训练和测试：

数据分布展示如下：

参考资料：

周志华 机器学习

字数限制可查看原文：https://blog.csdn.net/weixin_42633269/article/details/83035930