AIU人工智能学院：数据科学、人工智能从业者的在线大学。

数据科学（Python/R/Julia）数据分析、机器学习、深度学习

PCA最常见的应用之一就是将高维数据可视化，它可以将具有两个及以上特征的数据进行可视化，下面我们利用PCA来对cancer数据集进行可视化（良性肿瘤和恶性肿瘤），不使用PCA时可视化只能一个一个去对比其中的数据，其代码如下：

运行后结果如下：

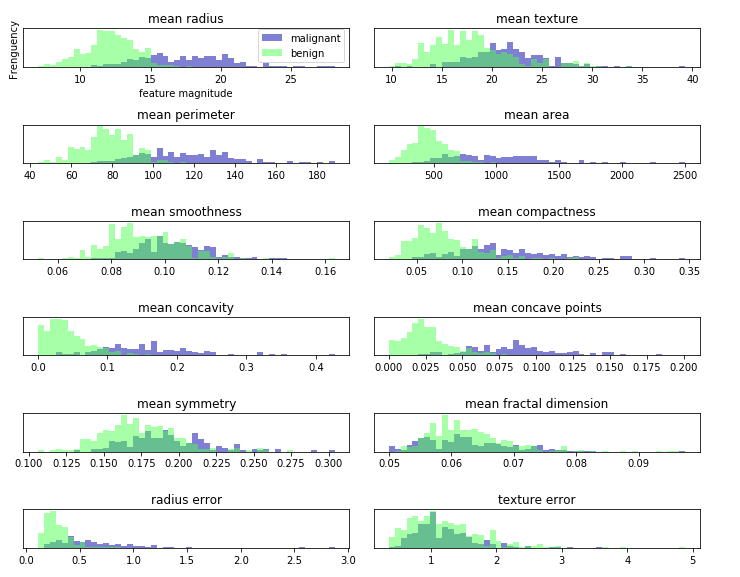
乳腺癌数据集中的类别直方图1

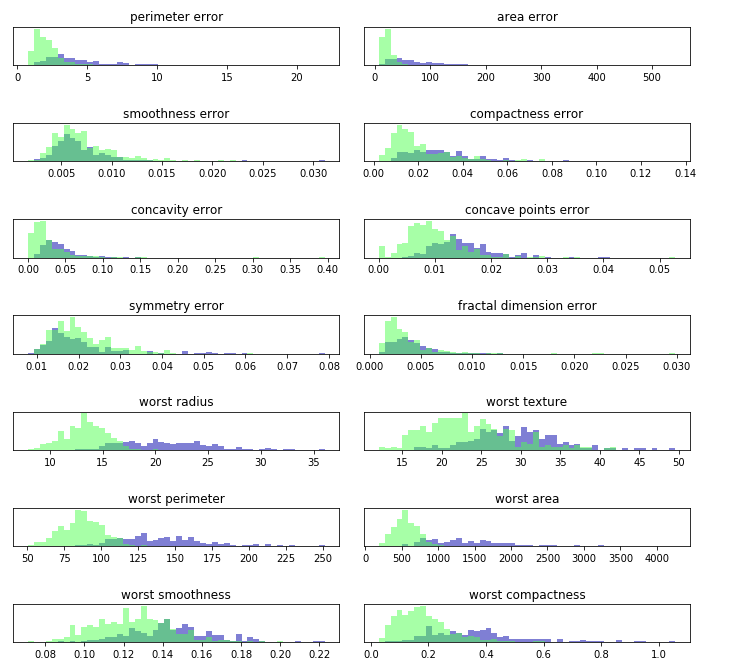
乳腺癌数据集中的类别直方图2

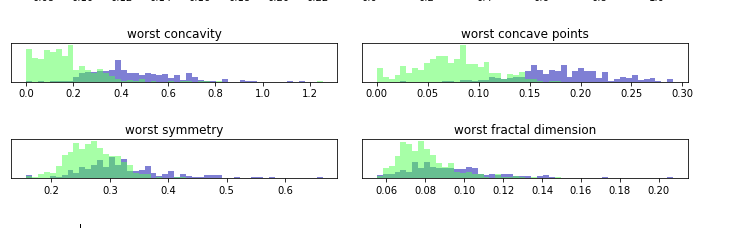
乳腺癌数据集中的类别直方图3

这里我们为每个特征创建一个直方图，计算具有某一特征的数据在特定范围内（叫做bin）的出现频率，。每张图都包含两个直方图，一个是良性类别（蓝色），一个是恶性类别，这样我们可以了解每个特征在两个类别中的分布情况，也可以猜测哪些特征能够更好地区分恶性和良性样本。如：“smoothness error”特征似乎没有什么信息量，因为两个直方图大部分都重叠在一起， 而“worst concave points”特征看起来信息量比较大，因为两个直方图的交集很小。

但是，这种图无法向我们展示变量之间的相互作用以及这种相互作用与类别之间的关系。利用PCA，我们可以获取到主要的相互作用，并得到稍微完整的图像，我们可以找到前两个主要成分，并在这个新的二维空间中用散点图来将数据可视化，其代码如下：

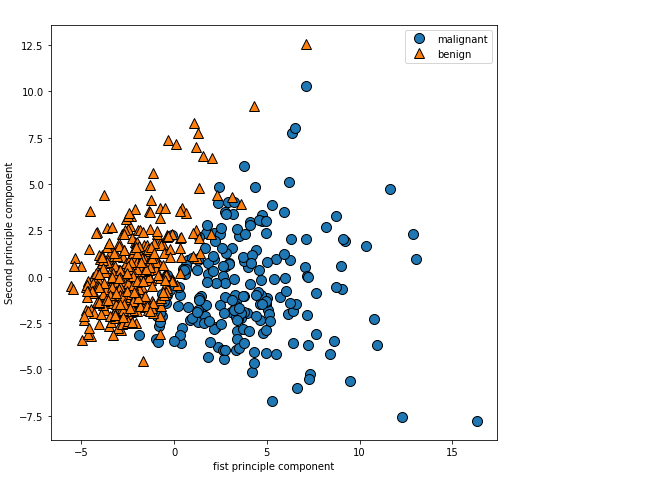
这里需要注意的是：PCA是一种无监督方法，在寻找旋转方向时没有用到任何类别信息，它只是观察数据中的相关性，并且将利用第一、二主成分的关系，绘制成图，由图可以看出，恶性点比良性点更加的分散。

PCA的一个缺点在于，通常不容易对图中的两个轴进行解释。主成分对应于原始数据中的方向，所以他们是原始特征的组合。但是这些组合往往非常复杂，这一点我们很快就会看到。在拟合过程中，主成分保存在PCA对象的components_.shape属性中，下节我们将对其进行讲解。

关注“AIU人工智能”公众号，回复“白皮书”获取数据分析、大数据、人工智能行业白皮书及更多精选学习资料！