一、背景

在平稳时序分析中，我们了解到平稳时序的概念和建模方法，但如果某时序是非平稳的呢？（即没有通过平稳性检验），那怎么办？传统时序分析中一般有两种手段：差分运算和确定性因素分解，针对这两种确定信息提取方式，可以分别构建两种传统模型：ARIMA和残差自回归模型。注意，本篇文章讲的基础是在残差序列具有同方差性上。下一篇文章会专门讲异方差残差序列的内容。

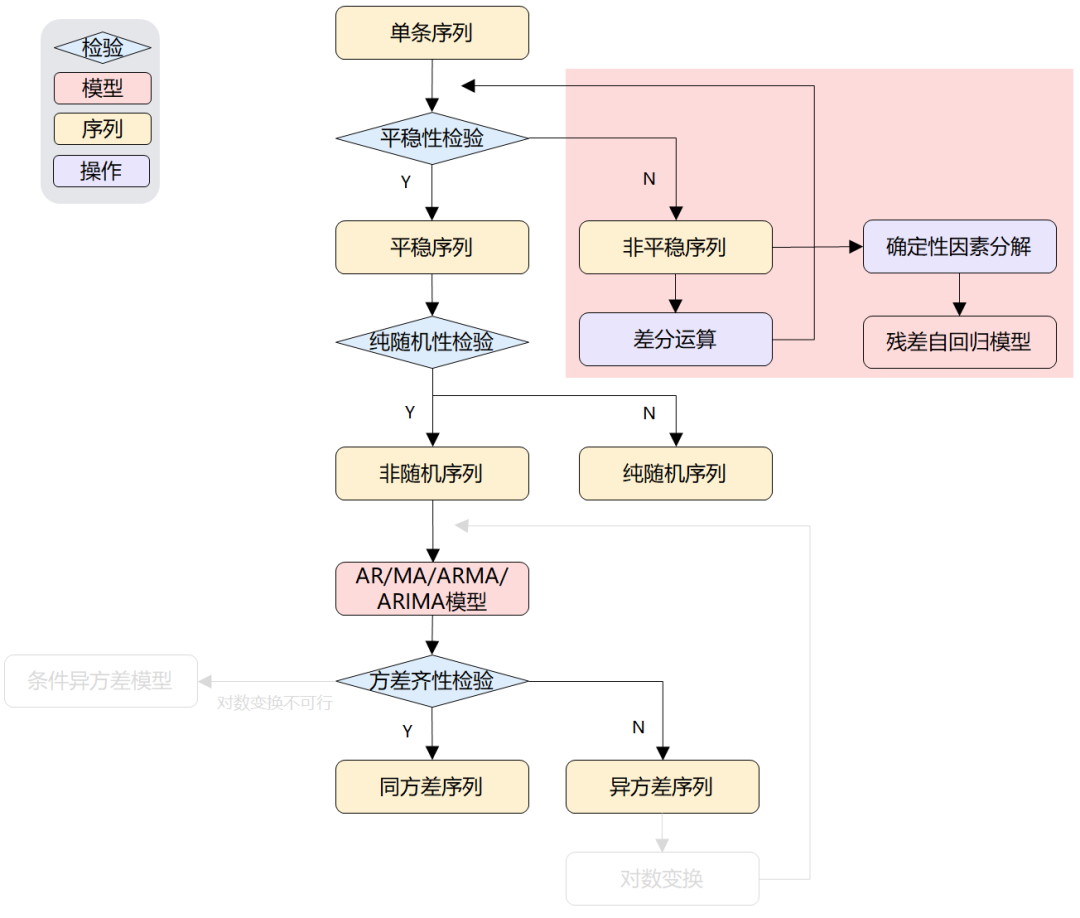
图1：非平稳时序（同方差）建模流程

二、差分运算

差分运算是一种十分简单有效的确定性信息提取方法，很多时候适当阶数的差分便可以充分提取出确定性信息。

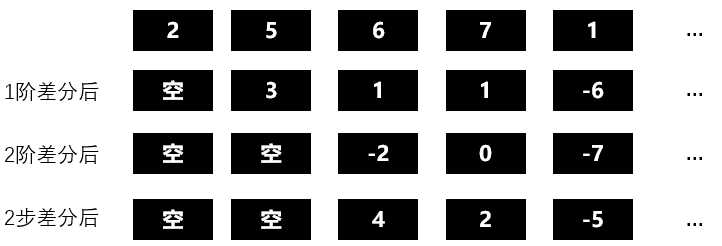
图2：多步多阶差分示意图

针对不同时序，我们可以选择不同差分方式，请见下图所示：

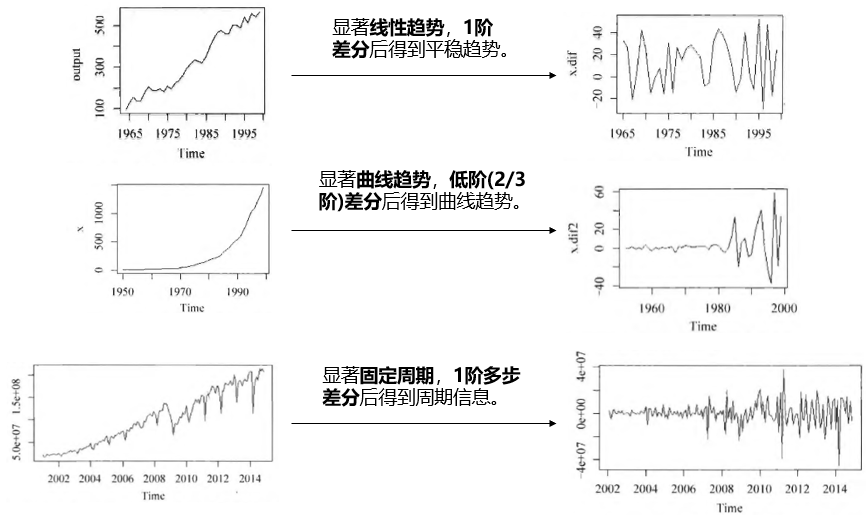
图3：不同非平稳时序的差分方法选择

三、ARIMA模型

差分可以将许多非平稳序列转为平稳序列，我们通常称之为差分平稳序列，对此，我们可以使用ARIMA模型（Autoregressive Integrated Moving Average model）进行拟合，该模型将差分运算与ARMA模型结合在一起，本质上就是差分后做ARMA模型。ARIMA有三个参数p、d和q，其中d为d阶差分。书中如图4的ARIMA建模流程跟图1是一样的：

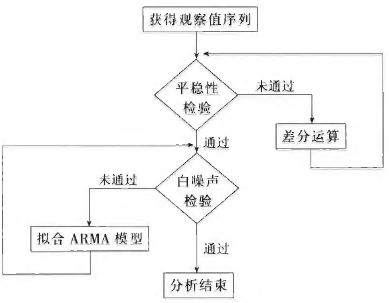
图4：ARIMA建模流程

四、确定性因素分解

除了差分运算，非平稳序列常会显示出非常明显的规律性：

● 长期趋势（Trend）：长期递增、递减等。

● 循环波动（Circle）：周期性/季节性反复循环波动。

● 随机波动（immediate）：消除趋势和周期变化后的随机影响。

1. 趋势

获取趋势有两种方法：

(1) 拟合法：线性拟合或非线性拟合。

(2) 平滑法：移动平均或指数平滑法。Python中statsmodel的序列趋势分解便是用的平滑法。

2. 季节

看季节/周期性，也有两种方法：

(1) 季节指数：反映该季度与总平均值之间的关系，若季节指数大于1，说明该季度的值常高于总平均值，若小于1，则反之，若近似等于1，说明该序列没有明显的季节效应。它分3步走：

(2) 去趋势求周期平均：Python中statsmodel的序列周期提取是先对原序列去除趋势项后，计算给定周期内的均值，用均值作为反映周期性。

3. 随机

若认为是加法模型形式，随机项=序列-趋势项-季节项。乘法模型，则通过除法获取随机项（有时也称残差项）。

五、残差自回归模型

残差自回归模型的中心思想很简单，就是先提取趋势项和周期项，再针对残差做AR模型。所以说它利用了确定性因素分解的方法，不同于差分提取非平稳序列中的确定性信息，确定因素分解将非平稳序列中趋势和季节提取出来了，而这样我们有：序列=趋势项+周期项+残差项，但有时候残差项可能也会具有确定性信息没被分解出来，因此残差自回归模型对残差做AR模型。

其中，对趋势项T的拟合有两种：

对周期项的拟合有两种：

那