理清基本概念的关系在开始看,我们先澄清几个该领域常见的容易混淆的概念:
AutoML, Bayesian Optimization (BO), Sequential Model Based Optimisation (SMBO), Gaussian Process Regression (GPR), Tree Parzen Estimator (TPE).
这些概念是啥关系呢:
AutoML BO SMBO {GPR, TPE}AutoML是最大的一个概念,涵盖了贝叶斯优化(Bayesian Optimization, BO)、神经结构搜索( Neural Architecture Search, NAS)以及很多工程性的东西。AutoML的目标就是让没有机器学习(这里包括深度学习)经验的人,可以使用某一个平台来构造、训练、使用机器学习模型,这个平台负责进行数据管理、模型结构设计、模型超参数调节、模型的评估与使用等等。
本文,也是我们搞深度学习的同学最关心的,就是模型超参数调节(hyper-parameter tuning)了。下面的所有概念都是围绕这个展开的。
贝叶斯优化(BO)则是AutoML中进行超参数调节的一种先进的方法,并列于人工调参(manul)、网格搜索(Grid Search)、随机搜索(Rrandom Search)。
SMBO则是贝叶斯优化的一种具体实现方法,是一种迭代式的优化方法,每一次的迭代就是一次新的超参数组合实验,而每次的迭代都是基于前面的历史。其实SMBO可以认为就是BO的标准实现,二者在很多语境下我感觉是可以等价的(这里我其实也不太确定,因为看了很多资料仿佛都是混着用,如果有朋友更清楚麻烦告诉我)。
最后就是Gaussian Process Regression (GPR) 和Tree Parzen Estimator (TPE) 了,这俩玩意儿是并列的概念,是SMBO方法中的两种建模策略。
以上,我们就先理清了这些概念的关系,然后,我们就可以更轻松地学习贝叶斯优化了。
下面,我们主要讲解这几个内容:
- 各种超参数调节方法的对比
- 贝叶斯优化/SMBO方法的基本流程
- 基于GPR的SMBO方法的原理
- 基于TPE的SMBO方法的原理
1. 各种超参数调节方法的对比超参数调节(hyper-parameter tuning),主要有下面四种方法:
- 人工调参(manul tuning)
- 网格搜索(grid search)
- 随机搜索(random search)
- 贝叶斯优化(Bayesian Optimization)
人工调参就不用说了,跑几组,看看效果,然后再调整继续跑。
Grid Search & Random Search这里简单对比一下grid search和random search:
 Grid Search vs. Random Search 来源:ResearchGate
Grid Search vs. Random Search 来源:ResearchGate上面是grid search和random search的示意图。简单地讲,random search在相同的超参数组合次数中,探索了更多的空间(这句话也有歧义,更准确得说应该是每个维度的参数,都尝试了更多的可能),因此从平均意义上看可以比grid search更早得找到较好的区域。
Grid Search
Random Search


上面这两个图(来自SigOpt)更加清楚一些,比方我们要找一个曲面的最高点,那我们按部就班地地毯式搜索,(有时候)就比我们东一榔头西一棒子地随机找要更慢,从理论上将,random search可以更快地将整个参数空间都覆盖到,而不是像grid search一样从局部一点点去搜索。
但是,grid search和random search,都属于无先验式的搜索,有些地方称之为Uninformed search,即每一步的搜索,都不考虑已经探索的点的情况,这也是grid/random search的主要问题,都是“偷懒式”搜索,闭着眼睛乱找一通。
而贝叶斯优化,则是一种informed search,会利用前面已经搜索过的参数的表现,来推测下一步怎么走会比较好,从而减少搜索空间,大大提升搜索效率。 某种意义上,贝叶斯优化跟人工调参比较像,因为我们调参师傅也会根据已有的结果以及自己的经验来判断下一步如何调参。
我们不要一提到贝叶斯就头疼,就预感到一大推数学公式、统计学推导(虽然事实上确实是这样),我们应该换一种思路:看到贝叶斯,就想到先验(prior)信息。 所以贝叶斯优化,就是一种基于先验的优化,一种根据历史信息来决定后面的路怎么走的优化方法。
所以贝叶斯优化的关键在于:用什么样的标准来判断下一步怎么走比较好。
2. 贝叶斯优化/SMBO的基本流程其实本文的主要内容,来自于超参数优化的经典论文"Algorithms for Hyper-Parameter Optimization",发表在2011年的NIPS上,作者之一是图灵奖得主Yoshua Bengio:
 Algorithms for Hyper-Parameter Optimization
Algorithms for Hyper-Parameter Optimization该文章介绍了SMBO的基本框架,以及GPR和TPE两种优化策略。
SMBOSMBO全名Sequential model-based optimization,序列化基于模型的优化。所谓序列化,是指通过迭代的方式,通过一次一次试验来进行优化。SMBO是贝叶斯优化的一种具体实现形式,所以下文中我们可能会直接把SMBO跟贝叶斯优化混着说。
SMBO的框架是这样的:
 SMBO框架伪代码
SMBO框架伪代码其中各个符号的意思如下:
- 是我们要去优化的函数,是超参数组合,比方我们要训练一个图片分类模型,那么每一个的选择,都会对应该分类模型的一个损失,这个函数关系就是. 一般,的计算都是十分耗时的;
- 是surrogate的缩写,意为“代理”,我们使用作为的代理函数,一般通过最小化来寻找下一步超参数怎么选,的计算一般会容易得多。一般这一步的最小化,我们是通过最大化一个acquisition function来进行的;
- 是history,是前面所有的{, }的记录,我们要对进行建模,得到它们的概率分布模型.
所以,总体步骤如下:
- 根据已有的调参历史,建立概率分布模型;
- 根据acquisition function来挑选下一步超参数;
- 将新的观测加入到中.
- 重复1-3步骤,直到达到最大迭代数
所以,不同的贝叶斯优化方法,主要区别在:
- 用何种概率模型对历史进行建模
- acquisition function如何选
对历史观测进行建模 对历史观测进行概率建模,来源:我自己画的假设我们已经尝试了一些超参数,也得到了一系列的值(即上图中的),这些点就是上图中的黑点,这些就是我们的历史信息。我们要优化的目标,肯定会经过这些历史观测点,但是其他的位置我们是未知的, 有无数种可能的会经过这些点,上图中的每一条虚线,都是可能的。所以各种可能的会形成一个函数的分布。我们虽然无法准确地知道的具体形式,但如果我们能够抓住其分布,那我们就可以了解很多该函数的性质,就有利于我们的趋势做一定的判断,从而帮助我们选择超参数。
对历史观测进行概率建模,来源:我自己画的假设我们已经尝试了一些超参数,也得到了一系列的值(即上图中的),这些点就是上图中的黑点,这些就是我们的历史信息。我们要优化的目标,肯定会经过这些历史观测点,但是其他的位置我们是未知的, 有无数种可能的会经过这些点,上图中的每一条虚线,都是可能的。所以各种可能的会形成一个函数的分布。我们虽然无法准确地知道的具体形式,但如果我们能够抓住其分布,那我们就可以了解很多该函数的性质,就有利于我们的趋势做一定的判断,从而帮助我们选择超参数。这就好比对于随机变量,虽然我们抓不住其确切的值,但如果知道其分布的话,那我们就可以得到其均值、方差,也就知道了该变量会在什么样的一个范围内波动,对该随机变量也就有了一定的掌握。
所以,贝叶斯优化中的一个关键步骤,就是对要优化的目标函数进行建模,得到该函数的分布 ,从而了解该函数可能会在什么范围内波动。另外,我们有了函数的分布,实际上也就有了y在给定x的时候的条件分布:
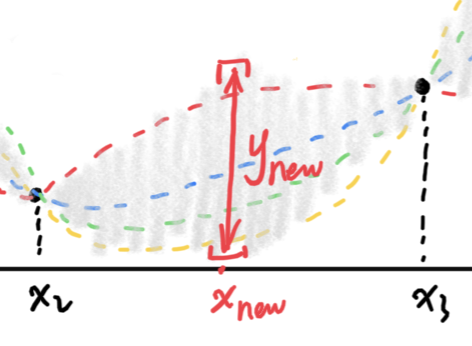 y在给定x时会有一个概率分布当给定一个新的超参数,的取值可以根据给出。
y在给定x时会有一个概率分布当给定一个新的超参数,的取值可以根据给出。具体的建模方法,最经典的包括高斯过程回归(GPR)和Tree Parzen Estimator(TPE),它们的细节会在后面的部分讲解。
Acquisition function / Expected Improvement (EI)我们继续看这个例子,假设我们的objective function就是loss,那么我们肯定希望找超参数使得loss最小,那么我们该如何根据该分布,来选择下一个超参数呢?
看下图:
 Exploration vs. Exploitation,来源:我自己画的已经观测到的点中,是最佳的超参数,那我们下一个点往哪个方向找?我们有两种策略:
Exploration vs. Exploitation,来源:我自己画的已经观测到的点中,是最佳的超参数,那我们下一个点往哪个方向找?我们有两种策略:- Exploitation(剥削?挖掘?使劲利用?):我们既然发现了最好,那估计周围的点也不错,所以我们在图中的area 1里面搜索;
- Exploration(探索):虽然处目前来看比较好,但是我们还没有探索到的空间实际还有好多好多,比方说图中的area 2区域,这里面很可能藏着惊喜!
实际上,上面两种策略各有各的道理,我们需要设计一个acquisition function来帮我们进行判断。一种最常用的方案就是Expected Improvement (EI),它是对Exploration和Exploitation做了一个折中。
Expected Improvement (EI)的公式如下:
其中是某个阈值,EI就是一个期望,该期望是的函数。当给定的时候,EI(x)就是相对于阈值平均提升了多少。(notice:这里我们都默认我们是要minimize目标函数,因此y的降低就是效果的提升;另外,实际上是一个我们需要指定的值,又是一个超参)也就是,我们首先有一个baseline——,我们就是通过计算EI——相对于的期望提升,来评价一个超参数的好坏。所以,我们下一步要找的超参数,就是:EI的公式决定了其偏好于选择均值小的、方差大的区域,因此就体现了"exploration vs. exploitation trade-off".

 扫码加好友,拉您进群
扫码加好友,拉您进群