给你一个附件吧，希望能对你有用~~~是关于赫斯特指数计算及相关说明的

百度百科就有关于赫斯特指数的说明，相当详细的，可以看看呗

Hurst 指数和重标极差法(R/S),通常用来分析时间序列的分形特征和长期记忆过程，最初由水文学家Hurst 在1951 年提出，Mandelbrot 在1972 年首次将 R/S分析应用于美国证券市场，分析股票收益的变化，Peters 把这种方法作为其分形市场假说最重要的研究工具进行了详细的讨论和发展，并做了很多实证研究（有兴趣的读者可以深入研究Peters的原著，Fractal Market Analysis Applying Chaos Theory to Investment and Economics）。
Hurst 指数可衡量一个时间序列的统计相关性。当 H =0.5 时，时间序列就是标准的随机游走(布朗运动），H=1时是线性状况。一般股票的Hurst指数在0.5和1之间，呈现有偏的随机过程。
学院派的Hurst指数论文,喜欢从头疯狂计算指数或个股的Hurst指数,结论往往类似: 市场有效假说是错误的 或者我国股票市场具有时间记忆特性。但这些结论对实际操作的意义不大，对股市操作有帮助的应是移动Hurst指数，这样能够体现股票或指数在最近阶段的状态特征。证券公司内部研究文章的结论是：Hurst指数小于0.55，往往是反转的标志。下图来自某证券公司的内部研究报告，上半图是上证指数的Hurst值，下半图是上证指数的对数图形。从图中可以看到，当上证指数的Hurst值低于0.55时，对应上证指数有反转的走势。



我只能看到证券公司的研究结论，但无法了解他们的计算方法。所以只能自己摸索和揣测，看看能否从自己的方式中找到对操作有帮助的结论。总之一切DIY。

计算Hurst指数的标准步骤如下：
对样本数量为M的价格序列{Pt}，定义N=M-1。首先得到其对数收益率:
          Xt = log（Pt+1 / Pt）， t=1，2，。。。 N
1. 将序列{Xt}分割成长度为n（n为整数）的A个子区间（1,2...N个连续数据一组)。计算每个子区间的均值Xpa和标准差Sa。
2.  计算每个区间中每个值的累计离差: Zi=(X1-Xpa)+...+(Xi-XPa) , i= 1,2...N
3.  定义每个区间的极差: Ra=Max(Zi)-Min(Zi)
4.  每个区间的重标度化极差: (R/S)n = (Ra/Sa)
5.  求分割长度为n时的平均重标度化极差
6.  对每个分割长度有如下关系式:
      log(R/S)n = Hlog(n)+ a   , n=1,2...N
     H就是Hurst指数,通过多组[log(n),log(R/S)n]可以估算出H的数值,通常使用最小两乘法来估算.
计算移动Hurst的简化方式(我的定义,不然计算速度太慢):
1.  只要对指定分割长度N计算标准步骤的前4部即可,得到log(R/S)n.
2.  令Hn = log(R/S)n / log(n)

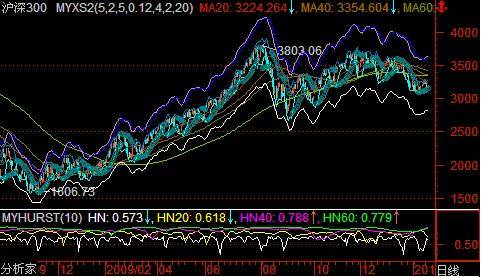
下图为对应的MyHurst指标和上证指数的对应图,周期较长的曲线比较平滑但滞后较严重,而周期短的曲线比较尖锐滞后小.
从图形来看,移动Hurst指标还是相当有效的反转指标,只要结合其他指标就可以形成较准确的买点和卖点.

我传一个我学习长记忆理论时用的参看文献吧
里面有介绍分型市场理论和相关检验  楼主可以认真的看一下

非常感谢A