空间计量研究中，如果为截面数据，可使用比如空间滞后模型、空间误差模型、空间杜宾模型等。当为面板数据时则稍有不同，面板数据进行空间计量分析时，主要有三个注意点，1是数据格式的整理，包括空间权重矩阵的数据格式和面板数据的数据格式（此处需要为平衡面板数据），以及空间权重矩阵与面板数据的ID匹配；2是面板模型的选择，是固定效应还是随机效应，应该使用Hausman检验进行检验并且得出结论；3是空间计量模型的选择，应该是面板滞后模型还是面板误差模型，此处默认提供LM检验得出结果。

• 关于第1点数据格式，如下所述：

  空间权重矩阵

  空间权重矩阵应该满足n*n阶格式，而且第1行为空间点的名称（比如31省市名称），类似如下图：

  
  

  面板数据

  面板数据即分析数据，其应该为平衡面板，比如31省市10年共计为31*10=310行数据，不能缺少某省市某年的数据，一定是31*10行数据。如果非平衡面板格式，SPSSAU会输出具体错误点便于进行排查。

  空间权重矩阵与面板数据ID的匹配

  比如31省市10年的数据，空间权重矩阵为31*31阶，但是面板数据是31*10=310行，那么二者如何去对应呢，比如空间权重矩阵里面的四川与面板数据里面的四川。SPSSAU在进行匹配时，是严格按照ID的数字大小先后顺序原则进行，即权重矩阵里面的顺序比如为：北京->天津->河北->山西…这样的顺序，那么面板数据里面的ID编号数字也要依从这样的顺序，建议研究者首先需要确保树重矩阵里面的空间点顺序，一定和面板数据里面空间点的数字大小顺序保持一致，比如下图：

  
  

  上图中左侧为权重数据例子，右侧为面板数据例子，SPSSAU在对权重矩阵和面板数据进行ID匹配时，其认为顺序为：北京->天津->河北->山西->内蒙古->吉林->….这样的顺序，那么面板数据的时候面板ID的数字大小顺序（注意是数字大小），也需要保持北京->天津->河北->山西->内蒙古->吉林->…这样完全一致的顺序。建议将面板数据ID按照权重矩阵里面的顺序依次编号为1，2，3类似这样的编号。（提示：面板ID不能使用文字格式，因为文字格式上传到SPSSAU中后会自动编码成数字并且打上标签，但原理上空间权重矩阵与面板ID的匹配是使用数字进行匹配；如果上传了文字数据，也可以使用数据编码功能对其进行编码成权重矩阵对应的空间点大小顺序）。

• 关于第2点Hausman检验

  在进行空间面板数据分析时，SPSSAU默认提供Hausman检验，便于确定应该使用面板固定模型还是面板随机模型，多数情况下可直接使用面板固定模型即可。

• 关于第3点空间计量模型选择

  当前默认输出LM检验，按照LM检验流程直接选择空间面板滞后模型或者空间面板误差模型，当然还有可能直接使用普通的面板模型进行分析即可，关于LM检验的判断逻辑如下图所示：

  
  

  空间面板模型时输出4个LM检验，首先针对LM-error和LM-lag进行分析，如果二者均不显著，则应该使用普通面板模型（即不考虑空间性），如果仅LM-error显著则使用空间面板误差模型，如果仅LM-lag显著则使用空间面板滞后模型，如果二者均显著，则需要进一步查看Robust LM检验；

  基于LM-error和LM-lag均显著时，则需要结合Robust LM-error和Robust LM-lag检验进一步判断，如果Robust LM-error和Robust LM-lag检验均不显著，此时退回到上一步即对比LM-error和LM-lag这两个检验对应的卡方值，哪个更大则使用更大对应的模型，比如LM-error检验的卡方值更大则使用空间面板误差模型，如果LM-lag检验的卡方值更大则使用空间面板滞后模型；如果仅Robust LM-error显著则使用空间面板误差模型，如果仅Robust LM-lag显著则使用空间面板滞后模型，如果Robust LM-error和Robust LM-lag检验二者均显著，此时可使用二者中对应卡方值更大时对应的模型（或者结合信息准则判断模型优劣），比如Robust LM-lag检验的卡方值比Robust LM-error检验时的卡方值更大，那么可使用空间面板滞后模型。

  除此之外，通常情况下，普通面板模型（即不考虑空间效应的面板模型）可作为一个参照模型与最终使用的空间模型进行对比分析。

  
  

• 1、背景

  当前有一份空间面板数据，其为美国1970~1974共5年48个州的面板数据，包括以下变量分别是gsp(州产出)，pcap(公共资本)，pc(民营资本)，emp(就业量)，现在希望研究州公共资本、民营资本和就业量对于州产出的影响作用关系，并且考虑空间作用。由于州产出gsp，公共资本pcap、民营资本pc和就业量emp这几个变量数字较大，因而对该4项分别取对数操作，最终部分数据如下图所示：

  
  

  上面展示的是‘分析数据’，Ln表示取对数的意思，可通过生成变量实现取对数处理，该数据共有48个州，该48个州对应的‘空间权重矩阵’如下图所示：

  
  

  图中数字1表示两个空间点（社区）之间相邻，数字0表示两个社区不相邻。需要特别注意的是，分析数据中state表示州的编号，从1到48，而且空间权重数据里面的id1,id2直到id48与该编号(state)保持一致，空间权重矩阵数据可点击此处下载。

  
  
• 2、理论

  空间面板模型时需要注意几个问题，一是数据格式，空间面板分析时需要为平衡面板数据且其id编号需要与权重矩阵里面的顺序保持一致性；二是空间计量模型的选择，具体应该使用空间面板滞后模型还是空间面板误差模型，应该结合LM检验进行决策；三是面板模型也包括FE固定效应和RE随机效应，具体应该由hausman检验进行判断。

  
  
• 3、操作

  本例子操作如下：

  
  

  将因变量和自变量放入对应框中，并且放好state和year（即面板数据的id和year两项），另空间模型类型上默认是滞后模型，具体应该空间面板滞后模型还是空间面板误差模型，建议以输出的LM检验进行判断和选择。另外下拉选择‘空间权重矩阵’文档即spatialpanelweight这份数据，默认对空间权重矩阵行标准化处理，需要注意的是，空间权重矩阵通常需要进行行标准化处理。

  另需要提示的是，在使用空间计量相关的方法时，其均需要‘空间权重矩阵’和‘分析数据’两份数据，并且均需要单独上传到SPSSAU中，并且对‘分析数据’进行分析时，下拉选择对应的‘空间权重矩阵’，操作上分为以下3个步骤。

  • 第1：上传‘空间权重矩阵’文档

    此处需要注意：上传的数据需要为n*n阶格式，而且第1行为空间点的名称（比如31省市的名称）。类似下图格式：

    
    

  • 第2：上传‘分析数据’文档

    此处需要注意：比如31省市数据，‘空间权重矩阵’有着该31个空间点的顺序比如北京-》天津-》河北-》山西-》…，那么‘分析数据’的31行数据也需要按此顺序才可以。

  • 第3：针对‘分析数据’进行分析，并且选择‘空间权重矩阵’文档

    此处需要注意：进行某空间研究方法时需要下拉选择‘空间权重矩阵’，选择后，SPSSAU会自动判断其是否为‘空间权重矩阵’格式，包括是否为n*n阶结构，是否具有对称性等。如果不是则会进行信息提示，请勿必注意空间权重矩阵数据格式。

    
    
  
  
• 4、SPSSAU输出结果

  SPSSAU共输出7个表格，分别是模型基本参数等、空间面板滞后模型分析结果、空间面板模型LM检验汇总、Hausman检验结果、信息准则指标结果、空间面板滞后模型相关检验汇总和空间面板滞后模型分析结果-简化格式，如下所述。

  表格	说明
  模型基本参数等	输出模型的基础参数值信息等
  空间面板滞后模型分析结果	输出模型的分析结果，包括回归系数和显著性检验结果等，并且包括面板固定效应和面板随机效应两个模型结果
  空间面板模型LM检验汇总	输出LM检验用于判断应该是空间面板滞后模型或者空间面板误差模型
  Hausman检验结果	输出Hausman检验结果用于判断面板固定FE效应模型还是面板随机RE效应模型
  信息准则指标结果	输出信息准则指标等
  空间面板滞后模型相关检验汇总	输出比如BP检验和JB检验等
  空间面板滞后模型分析结果-简化格式	输出模型结果的简化表格格式

  
  
  
• 5、文字分析
  

  上表格模型的基本参数信息，包括具体的空间计量模型名称，空间权重矩阵名称及是否对其进行标准化处理等，模型估计方法等，表格中仅展示模型的参数信息等无特别分析意义。

  
  

  上图展示空间面板模型时比较关键的四个检验，包括LM检验和稳健LM检验，并且分别分为LM误差检验和LM滞后检验；

  第一：首先针对LM-error和LM-lag进行分析，如果二者均不显著，则应该使用普通面板模型即可（即不考虑空间性），如果仅其中一个显著，比如仅LM-error显著则使用空间面板误差模型，如果仅LM-lag显著则使用空间面板滞后模型，如果二者均显著，则需要进一步查看Robust LM检验；

  第二：针对Robust LM-error和Robust LM-lag检验，如果仅其中一个显著，比如仅Robust LM-error显著则使用空间面板误差模型，如果仅Robust LM-lag显著则使用空间面板滞后模型，如果二者均显著，此时可使用二者中对应卡方值更大（此时p 更小）时对应的模型（或者结合信息准则判断模型优劣），比如Robust LM-lag检验的卡方值比Robust LM-error检验时的卡方值更大，那么可使用空间面板滞后模型，如果二者均不显著，此时可退回到LM检验进行综合判断。

  本案例数据时，首先分析LM-error检验和LM-lag，从上表可知：LM-error检验呈现出显著性(p =0.000<0.05)，并且LM-lag检验没有呈现出显著性(p =0.142>0.05) ，意味着此时使用空间面板误差模型较为适合。与此同时，还需要结合Hausman检验结果，用于判断应该使用面板固定效应模型或是面板随机效应模型，如下：

  
  

  上表格展示Hausman检验结果，从上表可知：Hausman检验并未呈现出显著性(Chi=-10.820，p =1.000>0.05)，意味着相对FE模型而言，RE模型更优。结合LM检验和Hausman检验结果，最终应该使用空间面板误差模型，并且应该使用随机RE模型结果作为最终结论。因而在选择模型时，应该下拉为空间误差模型，如下图所示：

  
  
  

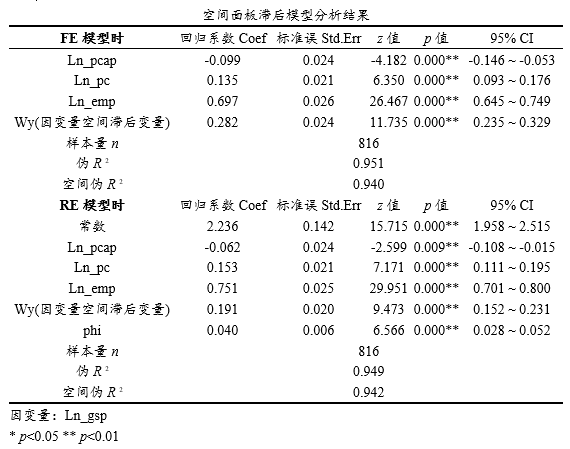
  上表格依旧展示的是空间面板滞后模型的结果，并且包括FE固定效应和RE随机效应时的结果具体解读上与普通回归的解读保持一致性，在面板滞后模型时，其模型中包括因变量空间滞后变量，其实际意义为其他地区对于本地区的影响。如果是面板误差模型时，其模型中包括误差项空间滞后项。

  
  

  上表格展示信息准则结果表格，包括llf值和另外两个值即AIC值和Schwarz准则值，llf值通常越大越好，但是AIC值和Schwarz准则值均是越小越好，如果希望对比模型优劣，可考虑使用上述三个指标，并且上述指标分为FE模型和RE模型均有提供。多数情况下并不需要关注上述指标。

  
  

  上表格展示BP检验和JB检验，分别用于异方差和正态性检验，空间计量模型时对于空间作用的关注力度明显最高，对于异方差和正态性关注度相对较低，从上表格可以看到，模型具有异方差和非正态性问题，但本文档暂不关注该两项。

  
  

  上表格展示模型的简化表格格式，并且区分为FE模型和RE模型时，并不再重复分析。

  
  
• 6、剖析
  • 涉及以下几个关键点，分别如下：

  • 空间面板计量分析时需要注意三点，分别是数据格式（包括空间面板需要平衡数据，及权重矩阵数据，以及二者的ID顺序需要保持一致或者相等），结合LM检验判断空间计量模型的选择，结合Hausman检验选择FE模型或者RE模型。

    
    
  
  
  

• 因变量空间滞后项或误差空间滞后项的意义？

• 如果是滞后模型则会有因变量空间滞后项，其实际分析意义为其他地区对于当前地区的影响作用关系；如果是空间误差模型则会有误差空间滞后项，其实际分析意义为模型无法解释的项即残差这个东西，其他地区对于当前地区的空间作用关系。