在空间计量模型的构建过程中，研究者往往需要在两类空间依赖性之间做出权衡：一类是源于变量间实际交互作用的空间溢出效应（如区域间的经济外溢），另一类则是由遗漏变量等因素引发的误差项空间相关性。面对这一选择，空间杜宾模型（SDM）与空间误差模型（SEM）提供了不同的建模路径。然而，当研究的核心既包含明确的自变量空间溢出预期，又必须应对潜在误差结构中的空间依赖问题时，一种融合二者优势的折中方案便显得尤为必要——这正是

空间杜宾误差模型（SDEM）的价值所在。

一、SDEM模型的理论逻辑：为何采用混合设定？

SDEM模型的关键在于对两种不同性质的空间依赖进行分离建模：

• 外生性空间溢出：这是研究关注的重点，属于结构性影响。它描述的是某一地区的解释变量如何通过空间传导机制影响邻近地区的结果变量。例如，周边城市的环保投入可能对本城的环境质量产生正向带动作用。
• 误差项的空间自相关：这是一种干扰性因素，通常源于未被观测但具有空间聚集特征的遗漏变量（如相似的地理条件或文化背景）。若不加以控制，可能导致估计偏差和推断失真。

该模型通过以下数学形式实现上述双重结构的表达：

y = Xβ + WXθ + u,    u = λWu + ε

我们可将其拆解为两个部分理解：

y = Xβ + WXθ + u —— 此部分与自变量空间滞后模型（SLX）一致。
其中，Xβ 表示本地自变量对本地因变量的直接影响；而WXθ 则捕捉了外部空间溢出效应，其系数θ 直接反映这种跨区域影响的强度与方向。

u = λWu + ε —— 这一部分沿用了空间误差模型（SEM）的设定，表明残差项u 存在空间自回归结构，λ 为对应的空间误差系数，ε 为独立同分布的经典扰动项。

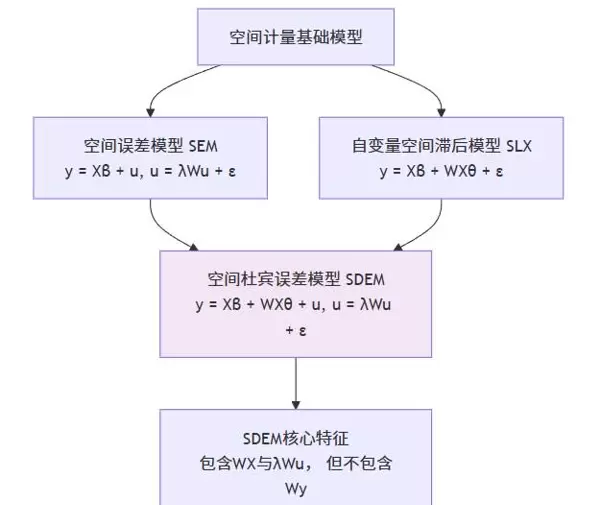
值得注意的是，SDEM与SDM的根本区别在于：不包含因变量的空间滞后项 Wy。这意味着模型并不假设被解释变量之间存在内生性的相互响应机制（如模仿或竞争行为）。因此，SDEM更适用于理论预设中仅存在外生空间互动的情境。

从模型谱系上看，SDEM可视作SLX与SEM的自然结合：既保留了对外生空间溢出（WX）的关注，也继承了对误差空间依赖（λWu）的控制能力，同时明确排除了因变量自身的空间反馈（Wy）。

二、SDEM的分析框架及SPSSAU输出解析

使用SPSSAU进行SDEM建模后，系统将生成一系列标准化结果表。准确理解这些输出内容，是正确解读模型含义的前提。

1. 模型基本信息表

作为报告的起始部分，此表格确保研究过程的透明与可复现。

其中清晰列出了所采用的模型类型为“空间杜宾误差SDEM模型”，并注明所用的空间权重矩阵、样本数量以及参数估计方法（如极大似然法ML）。这些信息构成了评估模型设定合理性的基础依据。

2. 回归参数估计表：核心结果呈现

该表格展示所有关键参数的估计值及其统计显著性。

• 自变量回归系数（β）：表示在控制了空间溢出和误差相关之后，本地解释变量对本地被解释变量的直接影响。
• 自变量空间滞后项系数（WX, θ）：直接衡量外生空间溢出效应的大小与方向，是验证研究假设的核心指标。若θ显著非零，则支持存在跨区域影响的判断。
• 空间误差系数（Lambda, λ）：反映误差项中空间依赖的程度。若λ显著，说明忽略此类结构将导致推断偏误，因而控制十分必要；反之，若不显著，则表明数据中此类干扰较弱。

重要说明：由于SDEM不含Wy项，其系数β和θ具备直接可解释性，无需像SDM那样进行复杂的空间效应分解。在此框架下，β可近似视为直接效应，θ则近似代表间接（溢出）效应。

3. 空间效应分解表：直观效应展示

尽管SDEM的原始系数已具解释力，SPSSAU仍会提供一张“空间效应分析”表格以增强结果表达的规范性。

由于模型未引入Wy所带来的动态反馈路径，效应计算相对简单：

• 直接效应 ≈ β
• 间接（溢出）效应 ≈ θ
• 总效应 = 直接效应 + 间接效应

该表的作用在于以统一术语（直接、间接、总效应）组织结果，便于与其他空间模型（如SDM）的研究成果进行横向对比。

4. 模型诊断与比较工具

为了辅助模型选择，SPSSAU还提供以下统计判据：

LR检验（似然比检验）：用于比较SDEM与其嵌套模型之间的拟合优劣。例如，检验原假设H: ρ=0（即SDEM优于含Wy的SDM）。若检验不显著（p > 0.05），则支持采用更简洁的SDEM；反之，则应考虑更复杂的SDM设定。

信息准则（AIC、SC）：在多个候选模型（如SDEM、SDM、SLX等）之间进行比较时，AIC与SC是重要的择优标准，一般遵循“越小越好”的原则。研究者可通过分别运行各类模型并比较其信息准则值，实现基于数据表现的最优选择。

三、SDEM模型的应用场景与实现路径

在何种情况下应当优先选用SDEM？主要取决于以下几个严谨的标准：

• 理论导向明确：研究假说聚焦于某种外生性的空间溢出机制，例如政策扩散、技术外溢或基础设施联动效应，而非因变量之间的内生互动。
• 需控制潜在遗漏变量偏差：存在理由相信某些未纳入模型的因素具有空间聚集性，可能污染误差结构，此时引入λWu有助于提升估计稳健性。
• 避免过度建模风险：相较于SDM，SDEM结构更为简洁，在缺乏充分证据支持因变量空间反馈的情况下，可防止模型过拟合。

综上所述，当研究目标强调解释变量的空间外溢且需兼顾误差结构稳健性时，SDEM提供了一个兼具理论清晰性与实证可靠性的理想选择。

空间杜宾误差模型（SDEM）通过融合外生变量的空间溢出效应（WX）与误差项中的空间依赖结构（λWu），同时排除因变量自身在空间上的内生互动（即Wy效应），构建了一个理论清晰且估计稳健的分析框架。该模型特别适用于研究重点聚焦于自变量空间外溢作用、并要求统计推断具备较高可靠性的实证情境。

在实际建模过程中，选择SDEM而非其他空间模型往往基于以下几个关键考量：

1. 理论导向的支持

当理论逻辑或研究假设并不支持被解释变量之间存在直接的空间反馈机制时，引入Wy项可能导致模型设定过度复杂甚至误导性解读。此时，忽略内生交互效应（Wy）而保留解释变量的空间滞后（WX），更符合研究问题的本质，使模型更具解释力。

2. 控制误差项的空间依赖以提升稳健性

为确保参数估计的有效性和推断的准确性，研究者常需处理残差中潜在的空间相关性。SDEM通过引入误差项的空间自回归结构（λWu），有效控制了由遗漏变量或测量误差引起的空间依赖问题，从而提高?θ?估计的稳健性，避免传统方法可能出现的偏误。

3. 模型比较结果的支持

借助LM检验、LR检验或AIC/BIC等信息准则进行模型对比后发现，SDEM在拟合优度上与SDM或SLX模型相当甚至更优，同时因其结构更为简洁，在避免过拟合方面具有优势。这种“简约而有效”的特性使其成为许多应用场景下的理想选择。

SPSSAU平台对SDEM模型的高效实现

SPSSAU为空间计量分析提供了专业且用户友好的操作路径，显著降低了SDEM模型的应用门槛：

• 明确的模型选项设计：在“空间计量”模块中，用户可直接选择“空间杜宾误差（SDEM）模型”，从入口层面保障了模型设定的准确性和针对性。
• 自动化完成复杂运算：系统自动执行包含空间误差结构的最大似然估计，并输出完整的分析结果，包括回归系数表、效应分解结果、各类检验统计量及信息准则值。
• 智能辅助决策功能：平台内置分析逻辑，能自动识别关键参数的显著性，并提供LR检验等功能，帮助用户科学地在SDEM、SDM等竞争模型之间做出判断。

总结

空间杜宾误差模型（SDEM）凭借其对外生空间溢出效应（WX）的关注与对误差项空间依赖（λWu）的有效控制，在兼顾理论合理性与估计稳健性方面展现出独特优势。它尤其适合那些旨在识别解释变量空间扩散效应、同时追求可靠统计推断的研究需求。

结合SPSSAU所提供的专业化分析工具，SDEM模型得以从复杂的数学设定转化为直观易用的操作流程。研究者无需深入编程或公式推导，即可高效完成模型拟合、结果解读与模型比较，进而从空间数据中精准提取结构性溢出效应，排除干扰性空间关联的影响。

在当前实证研究日益重视机制识别与估计稳健性的背景下，SDEM模型及其在SPSSAU中的便捷实现，正逐步成为区域科学、经济学、社会学等领域研究者手中不可或缺的重要分析手段。