摘要

本研究基于2023年10月至2025年11月期间沪深300指数的日度收盘价数据，利用EViews软件构建ARMA-GARCH混合模型，对指数收益率的波动性进行实证分析。首先验证了收益率序列具备平稳性、尖峰厚尾以及波动聚集等典型金融时间序列特征；随后通过ARMA(1,1)模型拟合其均值方程，发现残差存在显著的条件异方差性，进一步采用GARCH(1,1)模型有效刻画了波动率的时变性和持续性。结果表明，该组合模型能够较好地描述沪深300指数的动态变化路径，样本内预测虽存在一定误差，但未表现出系统性偏差。研究成果为理解A股市场波动机制及风险控制提供了有价值的参考依据。

关键词：沪深300指数；时间序列分析；ARMA模型；GARCH模型；波动率预测

引言

作为反映我国A股市场整体运行状况的重要指标，沪深300指数的波动特性受到投资者、监管机构和学术界的广泛关注。随着资本市场不断深化与开放，深入探究其内在波动规律并实现有效的波动率预测，在资产配置、风险管理以及政策制定等方面具有重要意义。

时间序列建模是分析金融市场动态的核心工具之一。其中，ARMA模型适用于处理平稳时间序列中的线性依赖关系，而GARCH模型则擅长捕捉“波动聚集”这一常见于金融数据的现象。近年来，ARMA-GARCH联合模型被广泛应用于股票指数、汇率等变量的研究中。本文在此基础上，选取2023年10月18日至2025年11月18日的沪深300指数日频数据，尝试建立合适的ARMA模型以提取均值过程，并结合GARCH模型刻画波动特征，最后开展样本内预测，评估模型的拟合效果与预测能力。

数据来源与预处理

研究所用数据为沪深300指数在2023年10月18日至2025年11月18日期间每日交易信息，包括开盘价、最高价、最低价、成交量和收盘价五个变量。分析过程中主要使用收盘价（close）序列进行后续建模。

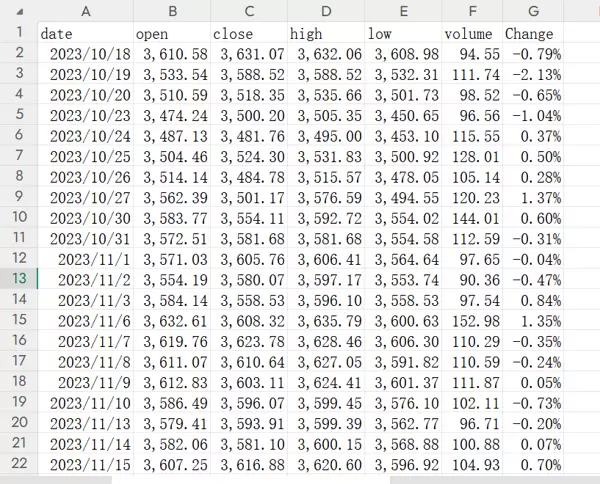
图2.1 数据展示图

经初步检查，日度交易数据在时间跨度上连续完整，无缺失记录。但注意到成交量字段带有单位“k”，需将其转换为纯数值格式以便导入EViews软件进行分析。数据清洗后录入EViews平台，形成如下工作文件视图：

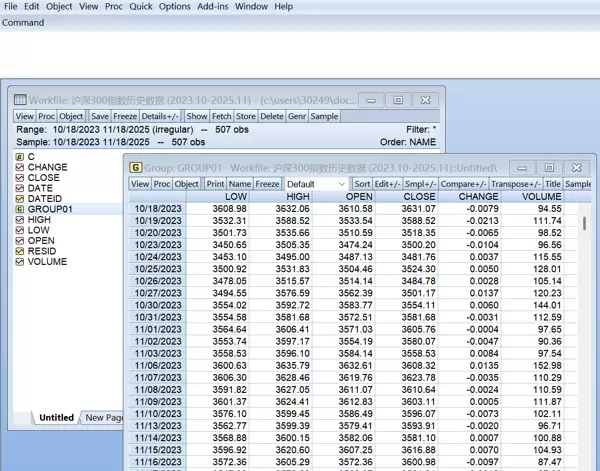
图2.2 EViews工作文件数据视图

收益率计算

在金融时间序列建模中，通常采用对数收益率来衡量价格变动，其计算公式为：rt = ln(Pt) - ln(Pt1)，即当前日与前一日收盘价自然对数之差。也可近似表示为 rt = (Pt - Pt1)/Pt1 × 100%。

在EViews命令窗口中执行以下指令完成收益率序列生成：genr r = (close - close(-1)) / close(-1) * 100

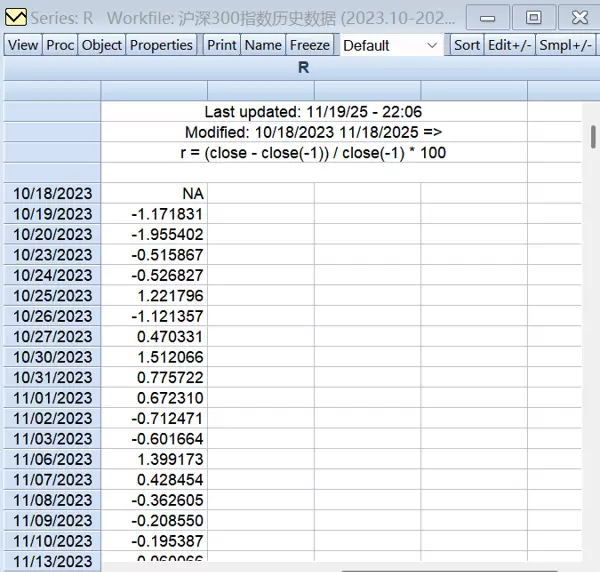
图2.3 收益率序列展示图

描述性统计分析

为初步识别收益率序列的分布特征，对其进行基本的描述性统计分析：

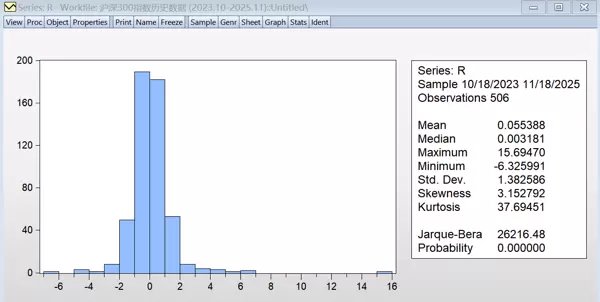
图2.4 收益率序列描述性统计

根据EViews输出结果，沪深300指数收益率呈现典型的非正态金融时间序列特征：偏度为3.15，表明分布右偏；峰度高达37.69，远大于正态分布的理论值3，说明存在明显的尖峰厚尾现象。Jarque-Bera检验统计量达26216.48（p值=0.000），强烈拒绝正态分布原假设。此外，从时序图可观察到明显的波动聚集效应，即高波动期与低波动期交替出现。

实证分析

平稳性检验

为满足ARMA类模型的应用前提，需确认收益率序列的平稳性。本文采用ADF（Augmented Dickey-Fuller）单位根检验方法进行判断。

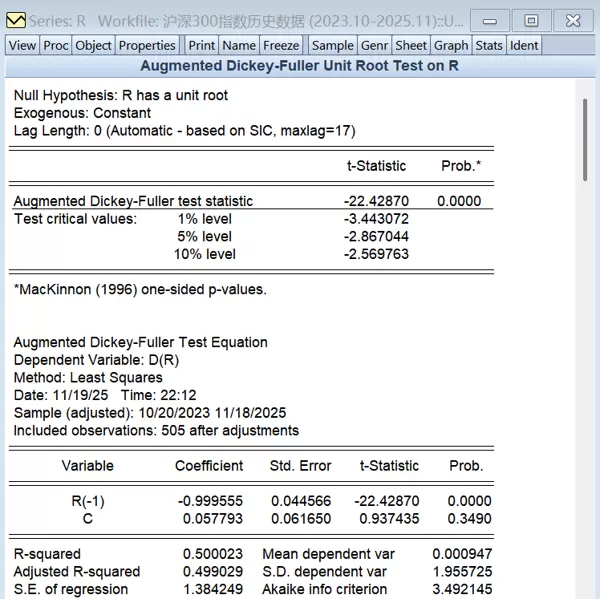
图3.1 ADF单位根检验结果

结果显示，收益率序列的ADF统计量为-22.42870，对应的p值为0.0000，远低于常用显著性水平，因此可以强烈拒绝“存在单位根”的原假设，表明该序列是一个平稳时间序列，符合建立ARMA模型的基本条件。

ARMA模型识别与建立

模型定阶：ACF与PACF分析

为进一步确定ARMA模型的具体阶数，绘制收益率序列的自相关函数（ACF）与偏自相关函数（PACF）图进行识别：

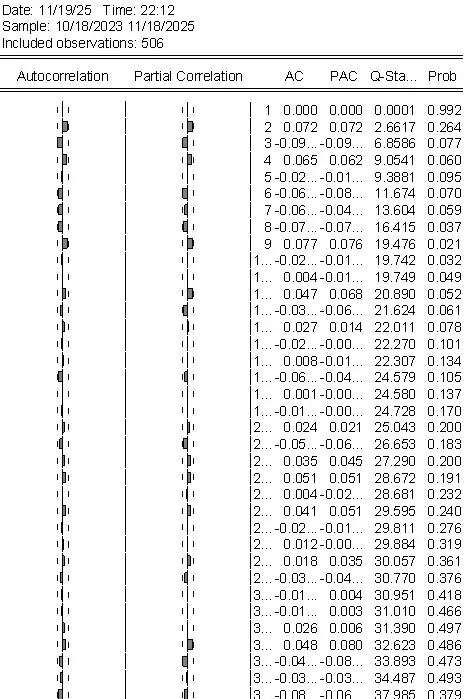
图3.2 收益率序列相关图 (ACF & PACF)

从图形来看，ACF在滞后一期后迅速衰减进入置信区间，多数自相关系数不显著；PACF同样在滞后一期后趋于截尾，仅在滞后3、6、8期等个别位置出现轻微显著的负向偏自相关系数。具体数值显示，ACF在滞后2期（0.072）、滞后4期（0.065）、滞后9期（0.077）有小幅波动，但均未突破显著性边界；PACF在滞后3期（-0.091）、滞后6期（-0.085）、滞后8期（-0.072）出现相对突出的峰值。

综合判断，该序列的相关结构符合低阶ARMA过程的特征，最终选择ARMA(1,1)模型作为均值方程较为合理。

根据AIC与BIC信息准则的综合分析结果，最终选定ARMA(1,1)模型作为最优模型。该选择不仅有效捕捉了时间序列的自相关结构，同时避免了参数过多带来的过度拟合问题，为后续构建ARMA-GARCH混合模型提供了可靠的均值方程基础。

ARMA模型的建立

在确定采用ARMA(1,1)模型后，使用最大似然估计法对模型参数进行估计。

模型设定

ARMA(1,1)模型的一般表达式如下：

其中，rt 表示第t期的收益率，c 为常数项，?1 为自回归系数，θ1 为移动平均系数，εt 为白噪声误差项。

参数估计

通过最大似然估计方法，在EViews中输入命令“ls r c ar(1) ma(1)”进行估计，得到以下结果：

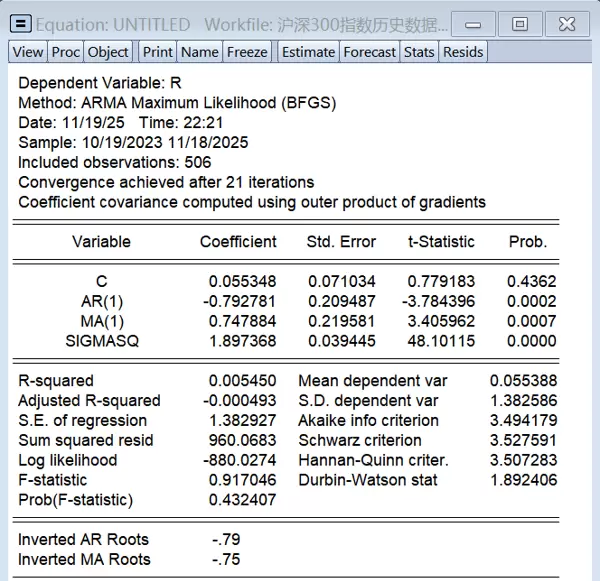
图3.3 ARMA(1,1)模型估计结果

具体估计输出如下：

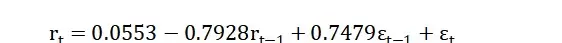
从回归结果可以看出，所有参数的t统计量均通过显著性检验，表明模型设定合理。此外，倒置AR根为-0.79，倒置MA根为-0.75，均位于单位圆内，满足平稳性与可逆性条件，进一步验证了模型设定的恰当性。

因此，该ARMA(1,1)模型成功提取了沪深300指数收益率的动态特征，为后续构建GARCH模型奠定了良好的均值方程基础。

条件异方差检验与GARCH建模

ARCH效应检验

为判断是否存在波动聚集现象，对ARMA(1,1)模型的残差序列进行ARCH-LM检验，结果如下：

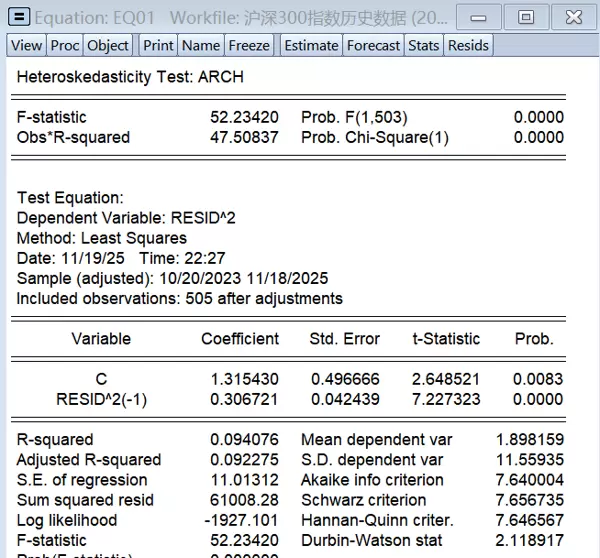
图3.4 ARCH-LM检验结果

检验结果显示：F统计量为52.234（p=0.0000），Obs*R-squared 统计量为47.508（p=0.0000），均在1%水平上拒绝无异方差原假设。同时，残差平方的一阶滞后项系数为0.307（t=7.227，p=0.0000），显著为正，说明残差中存在明显的ARCH效应，即波动率具有显著的聚类特征。因此，有必要引入GARCH模型来刻画沪深300指数收益率的条件异方差性。

GARCH模型构建

基于上述检验结果，本文构建GARCH(1,1)模型以描述沪深300指数的波动特性。在EViews中输入命令：equation eq_garch.arch(1,1) r c，获得估计结果如下：

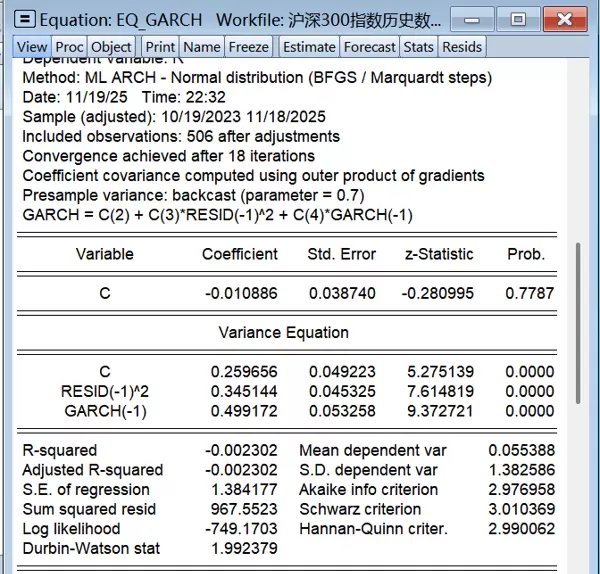
图3.5 GARCH(1,1)模型估计结果

模型在18次迭代后收敛，方差方程中的各项参数均在1%水平上高度显著，说明GARCH模型能有效捕捉收益率的波动行为。

均值方程分析

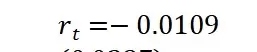
结果显示，常数项z = -0.281（p = 0.779），不显著，表明沪深300指数收益率序列没有明显的均值回复或趋势成分，符合有效市场假说的基本预期。

方差方程分析

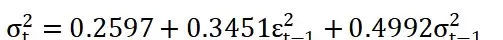
ARCH项系数为0.3451（z = 7.615，p = 0.000），说明前期冲击对当前波动率有显著正向影响，利好或利空消息均会引发市场波动上升；GARCH项系数为0.4992（z = 9.373，p = 0.000），反映出波动率具有较强的持续性。

从波动持久性角度看，α + β = 0.3451 + 0.4992 = 0.8443 < 1，满足平稳性要求，意味着外部冲击的影响虽会随时间衰减，但持续时间较长。

模型拟合效果评估

模型的对数似然值为-749.1703，AIC = 2.977，BIC = 3.010，相较于仅使用ARMA模型时明显降低，说明加入GARCH结构后模型拟合优度显著提升。

GARCH(1,1)模型有效刻画了沪深300指数收益率的波动聚类和持续性特征，为风险测度、资产定价及投资组合优化提供了有力的量化支持。

模型诊断与预测表现

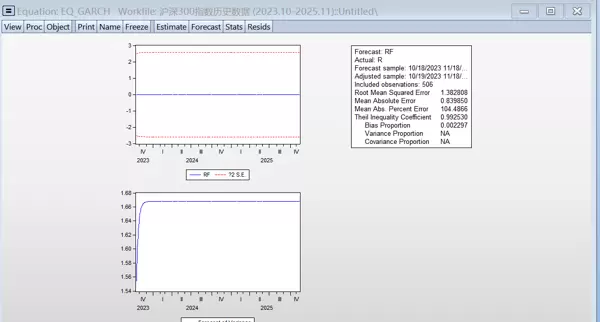
图3.6 模型样本内预测效果评估

基于GARCH模型的样本内预测结果，预测误差指标显示：均方根误差（RMSE）为1.383，平均绝对误差（MAE）为0.940，Theil不等系数为0.993，整体拟合效果尚可。偏差比例仅为0.002，表明模型不存在系统性预测偏误，能够较好地反映收益率序列的动态变化规律。

研究结论与建议

结论

实证分析表明，沪深300指数收益率具备典型的尖峰厚尾和波动聚集特征。ARMA(1,1)-GARCH(1,1)模型能有效拟合其动态路径，波动率的持续性指标α+β=0.8443，接近但小于1，验证了该模型在我国主要股指波动建模中的适用性和稳健性。

建议

对于投资者而言，可借助GARCH模型动态监测市场波动，在高波动时期及时调整仓位与风控策略；金融机构可将该模型纳入风险管理框架，提高VaR等风险度量工具的准确性。

监管部门亦可考虑将模型生成的条件波动率作为辅助性市场风险监测指标，为防范系统性金融风险提供参考依据。

未来研究可进一步拓展至非对称GARCH类模型（如EGARCH、TGARCH）以及跨市场波动溢出效应的分析，以深化对中国资本市场波动传导机制的理解。

本文综述了近年来关于金融市场波动性、股指期货影响以及经济结构与产业发展的多项实证研究。通过对相关文献的梳理，揭示了不同金融工具对市场运行特征的作用机制，同时也反映了统计模型在经济分析中的广泛应用。

在股票市场波动性研究方面，多位学者采用了GARCH族模型进行建模与检验。例如，张慧（2024）基于ARMA-GARCH模型对中国股票市场收益率的波动性进行了实证分析，揭示了波动聚集性和杠杆效应的存在。 同样地，顾鑫（2020）和宋小宇（2019）也分别运用GARCH模型探讨了我国股市收益波动的动态特征，进一步验证了该类模型在刻画金融时间序列非线性特性方面的有效性。此外，谢赤与贝籽（2014）采用门限GARCH（TR-GARCH）模型研究了中央银行外汇干预行为的波动传导特征，拓展了GARCH模型的应用场景。

关于股指期权及股指期货对现货市场的冲击效应，已有大量研究从不同角度展开。尹丽敏（2024）考察了中国股指期权上市后对股票市场波动性的影响，发现其在初期带来了波动率的结构性变化。而针对沪深300股指期货的研究更为丰富：胡德建（2015）、方欢（2013）以及刘超等（2011）均通过事件研究法或对比分析发现，股指期货推出初期可能加剧市场波动，但长期有助于价格发现和风险对冲。牟苏婵（2011）则比较了仿真交易与正式交易阶段的影响差异，指出制度完善对稳定市场的重要作用。

在市场间联动关系方面，赵庆全（2021）和姚清（2019）分别研究了可转债市场与股票市场之间的波动溢出效应，结果表明两个市场存在显著的双向波动传导，尤其在政策调整或市场动荡时期更为明显。 此外，关莉（2021）和赵锦洲、王泳波（2016）聚焦于沪深300股指期货对现货市场流动性的影响，采用PSM与DID等准自然实验方法，得出期货交易整体上提升了现货市场的流动性和定价效率。

除金融市场内部机制外，部分研究还关注宏观经济层面的问题。徐航（2022）利用R语言对中国产业结构变迁对经济增长的贡献进行了量化分析，强调服务业升级和技术进步的关键作用。王雪然（2017）则对“三驾马车”即投资、消费与出口拉动经济增长的过程进行了结构性突变检验，发现我国经济增长动力存在阶段性转换特征。陈伟（2018）从资源环境约束视角出发，探讨了高耗能产业转移的驱动因素，为区域协调发展提供了政策参考。

在风险管理领域，李蕊（2010）将VaR方法结合PARCH模型应用于开放式基金的风险测度中，结果显示考虑厚尾与非对称性的模型能更准确评估极端损失概率。这一研究为金融机构的风险控制提供了实用工具支持。

最后，刘君伟与杨晓辉（2024）将ARMA模型应用于隧道变形预测中的参数估计问题，展示了时间序列模型在非金融领域的延伸应用潜力，体现了计量方法的跨学科价值。