小波包获得某个节点信号的几个细节问题

jingweimo

4157

收藏 2013-10-10

小波包分解主要用了这四个函数 wpdec,wprec,wprcoef,wpcoef。

1）Wpcoef：
求解某个节点的小波包系数，数据长度是L/(2^n)（n表示分解的层数）
比如：原始信号长度为1024，经过3层分解，则使用cfs=wpcoef(wpt,[3 0])得到128个数据点，用以描述原始信号的近似低频信息。
具体代码如下：

clc;

% clear all;

close all;

load noisdopp; x = noisdopp;

% Decompose x at depth 3 with db1 wavelet packets

% using Shannon entropy.

wpt = wpdec(x,3,'db1');

plot(wpt); % Plot wavelet packet tree wpt.

cfs = wpcoef(wpt,[3 0]);

figure;

subplot(211);

plot(x); title('Original signal');

subplot(212);

plot(cfs); title('Packet (3,0) coefficients');

运行效果图如下所示：

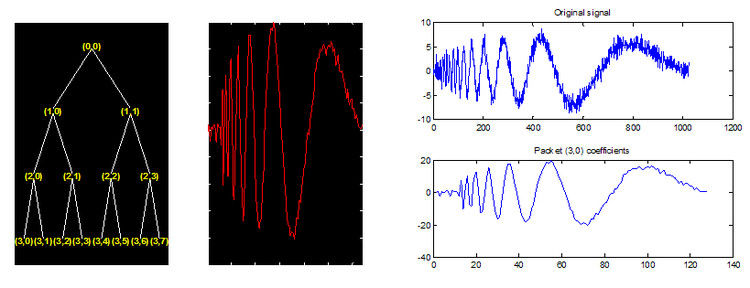
原始信号长度为1024，经过3层分解后，原始信号的近似信号长度为128。但是，为什么c(3,0)包数据的幅值会比原始信号大，后面会作具体研究。
2）Wprcoef：
把某个节点的小波包系数重构，得到的是和原信号一样长度的信号。
具体代码如下：

% clear all;

close all;

load noisdopp; x = noisdopp;

% Decompose x at depth 3 with db1 wavelet packets

% using Shannon entropy.

t = wpdec(x,3,'db1','shannon');

plot(t); % Plot wavelet packet tree.

rcfs = wprcoef(t,[3 0]);

figure(2);

subplot(311);

plot(x); title('Original signal');

subplot(312);

plot(rcfs); title('Reconstructed packet 3,0)');

运行效果图如下所示：

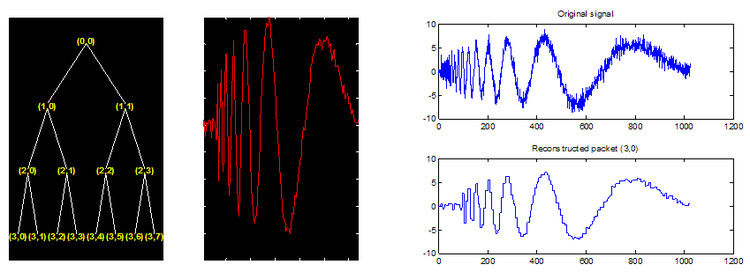
  原始信号长度为1024，使用rcfs = wprcoef(t,[3 0])得到的近似信号长度为1024，不同于cfs = wpcoef(wpt,[3 0])。
  3）分析wprcoef与wpcoef的异同
在本例中，原始信号长度为1024。使用wprcoef得到rcfs，其长度为1024；而使用wpcoef得到cfs，其长度为128。
为了方便显示，将上述组数据导入LabVIEW软件，通过波形图直观地查看这几组数据之间的区别。
将上述原始信号，rcfs，cfs信号存至Excel中，则使用如下命令：
   >> xlswrite('C:\compare.xls',noisdopp','sheet1','A1');

>> xlswrite('C:\compare.xls',rcfs','sheet1','B1');

>> xlswrite('C:\compare.xls',cfs','sheet1','C1');

在LabVIEW软件中使用Report Generation Toolkit导入这三组数据，分别命令：original data,rcfs data,cfs data。

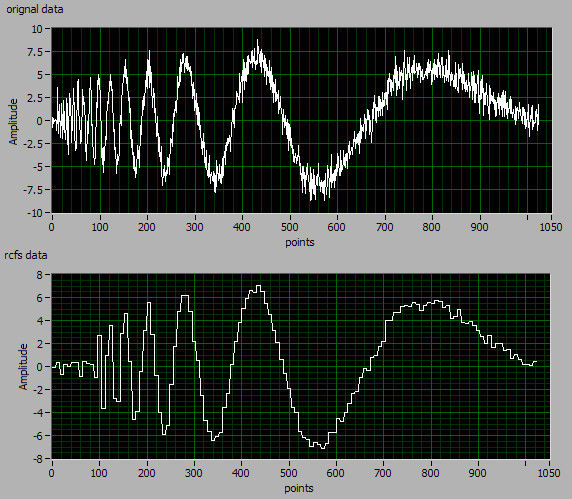
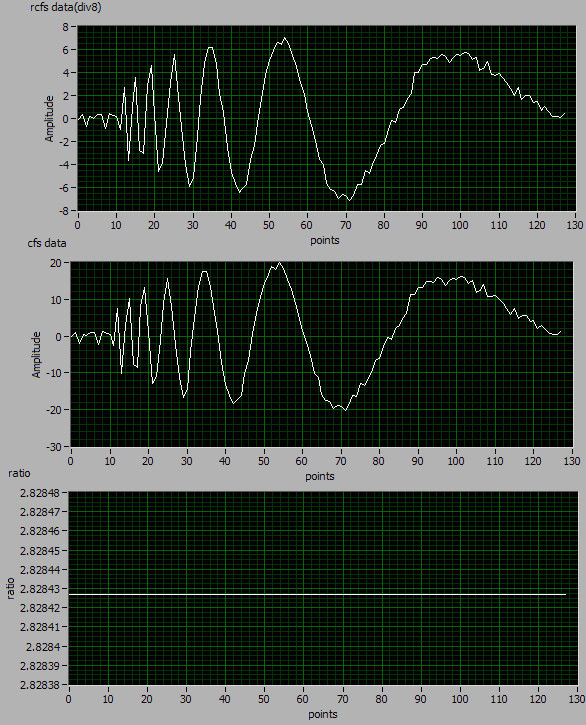
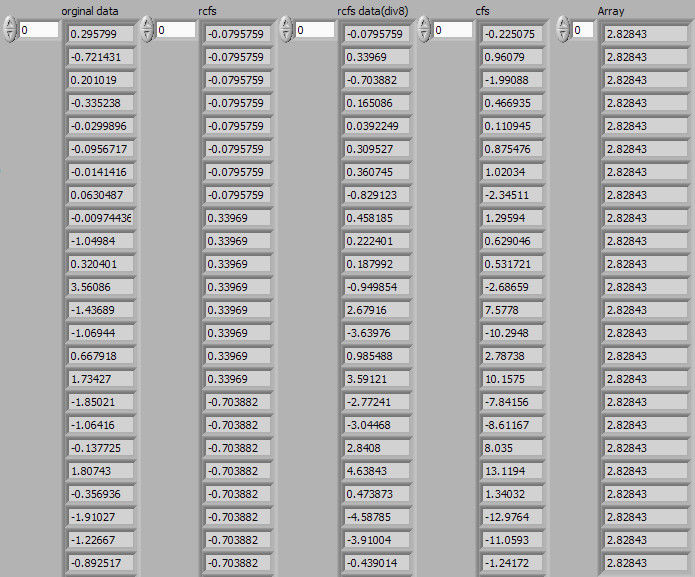
在上图中，将cfs data和rcfs data(div8)作商，得到的商的值均为2.82843（恒值）。
结论：
wprcoef和wpcoef使用不同的方式对原始信号做小波包分解，均可实现对原始信号的分解，某一个节点处的信号的提取。不同的是使用wprcoef得到rcfs，其长度为1024；而使用wpcoef得到cfs，其长度为128。将rcfs信号作8分频，其大致曲线一致，只是幅值不同。
疑问：

为什么使用cfs = wpcoef(wpt,[3 0])得到的分解信号，相对于原始信号，其幅值均增加至原始幅值的2.82843倍，有待进一步研究。

附录：

几组信号的实际数据对比图：