Fractional Brownian Motion_An Introdction with Necessary Mathmatics Tools: Malliavin Caculus and Wick Product

Fractional Brownian Motion

        A normalized fractional Brownian motion (fBm), also called a fractal Brownian motion, is a generalization of  Brownian motion without independent increments. It is a continuous-time Gaussian process BH(t) on [0, T], which starts at zero, has expectation zero for all t in [0, T], and has the following covariance function:

.

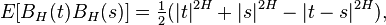        Where H is a real number in (0, 1), called the Hurst index or Hurst parameter associated with the fractional Brownian motion. The Hurst exponent describes the raggedness of the resultant motion, with a higher value leading to a smoother motion. It was introduced by Mandelbrot & van Ness (1968).

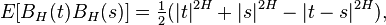
        The value of H determines what kind of process the fBm is:if H = 1/2 then the process is in fact a Brownian motion or Wiener process;if H > 1/2 then the increments of the process are positively correlated;if H < 1/2 then the increments of the process are negatively correlated.The increment process,X(t) = BH(t+1) − BH(t), is known as fractional Gaussian noise.

        Prior to the introduction of the fractional Brownian motion,Lévy (1953) used the Riemann–Liouville fractional integral to define the process:

        Where integration is with respect to the white noise measure dB(s). This integral turns out to be ill-suited to applications of fractional Brownian motion.The idea instead is to use a different fractional integral of white noise to define the process: the Weyl integral

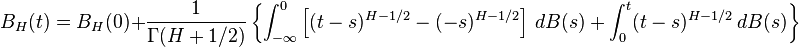
        The main difference between fractional Brownian motion and regular Brownian motion is that while the increments in Brownian Motion are independent.

具体分数布朗运动及其在金融中应用文献可见

本帖隐藏的内容

https://bbs.pinggu.org/thread-3189718-1-1.html
https://bbs.pinggu.org/thread-3197055-1-1.html

Wick Products or Wick Intergral:分析分数布朗运动不可缺少的数学工具之一

具体关于Wick Products的文献可见

本帖隐藏的内容

A note on Wick products.pdf
大小:(131.53 KB)

 马上下载

Malliavin calculus:分析分数布朗运动不可缺少的数学工具之二

        The Malliavin calculus, named after Paul Malliavin, extends the calculus of variations from functions to stochastic processes. The Malliavin calculus is also called the stochastic calculus of variations. In particular, it allows the computation of derivatives of random variables.            

        Malliavin ideas led to a proof that Hörmander's condition implies the existence and smoothness of a density for the solution of a stochastic differential equation; Hörmander's original proof was based on the theory of partial differential equations. The calculus has been applied to stochastic partial differential equations as well.        

        The calculus allows integration by parts with random variables; this operation is used in mathematical finance to compute the sensitivities of financial derivatives. The calculus has applications for example in stochastic filtering.       

具体关于Malliavin Caculus的文献与书籍可见

本帖隐藏的内容

AN INTRODUCTION TO MALLIAVIN CALCULUS WITH APPLICATIONS TO ECONOMICS.pdf
大小:(396.88 KB)

 马上下载

Stochastic Calculus for Fractional Brownian Motion and Related Processes.pdf
大小:(2.88 MB)

 马上下载

Malliavin Calculus for Processes with Jumps.pdf
大小:(10.12 MB)

 马上下载

Applications of Malliavin calculus to the pricing and hedging of Bermudan options.pdf
大小:(551.69 KB)

 马上下载

(百慕大期权定价)