CDA数据分析师：数据科学、人工智能从业者的在线大学。
数据科学（Python/R/Julia）数据分析、机器学习、深度学习

上节我们介绍了线性回归和Ridge回归，并介绍了两种回归的优缺点。本节我们重点学习下lasso回归的方法和优缺点。

和岭回归（Ridge）回归一样，lasso回归也是一种正则化的线性回归，且也是约束系数使其接近于0，不过其用到的方法不同，岭回归用到的是L2正则化，而lasso回归用到的是L1正则化（L1是通过稀疏参数（减少参数的数量）来降低复杂度，即L1正则化使参数为零，L2是通过减小参数值的大小来降低复杂度，即L2正则化项使得值最小时对应的参数变小）。

下面我们来看将lasso正则化运用到波士顿房价数据集上的效果，对应代码如下：

上述代码运行结果如下：

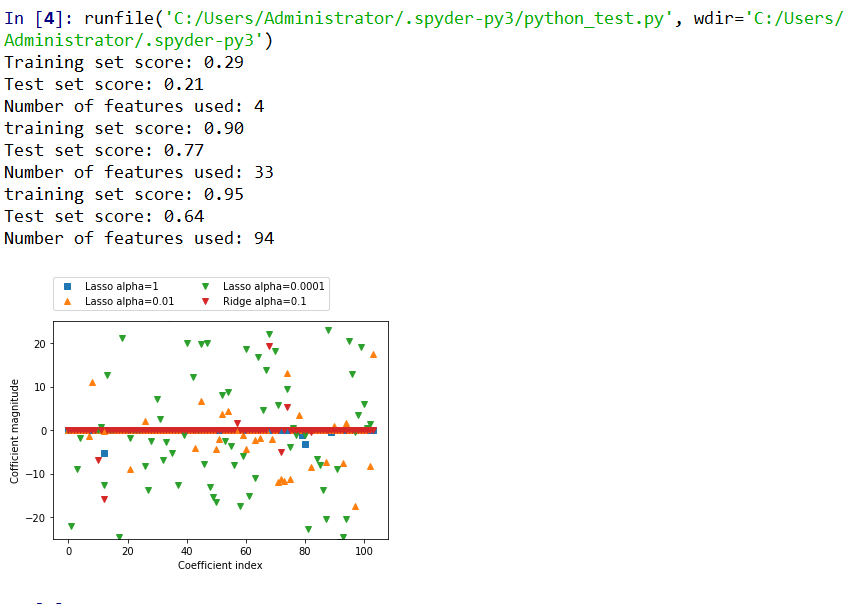
不同alpha值得lasso和岭回归（ridge）的系数比较

由上述代码我们可以看出，当使用特征数比较少时，lasso的训练集和测试集表现都很差，这表示存在欠拟合。通过调整alpha值，可以控制系数趋向于0的强度。当我们将alpha值变小，我们可以拟合一个比较复杂的模型，此时，训练集和测试集反而表现得更好，当我们将特征值从4个上升到33个是，训练集和测试集已经表现得比较好了。不过，如果将alpha值设置得太小的时候，训练集就会远大于测试集了，这是就出现了过拟合的情况。

在实践中，岭回归（Ridge）和lasso我们首选岭回归。不过如果特征数过多，但是其中只有几个特征是重要的，则选择lasso效果会更好。同时，lasso由于其模型更加便于理解（因为它只选择一部分输入特征），所以有时候用lasso回归效果也不错。当然，如果我们能够将两者进行优势互补，则会达到更佳的效果，在scikit-learn中提过了ElasticNet类，就是结合了这两种回归的惩罚项。在实践中效果会更好，不过需要同时调节L1和L2正则化参数，在以后章节中我们会介绍到。