一、条件极值概述

无其他条件求多元函数的极值，有时候称为无条件极值。

但在实际问题中，有时会遇到对函数的自变量还有附加条件的极值问题，称为条件极值。

例如，求表面积为a^2而体积为最大的长方体的体积问题。设长方体的三棱长分为x、y、z，那么体积V=xyz。又由表面积条件，有2(xy+yz+xz)=a^2。此类条件极值可转化为无条件极值问题。即根据表面积条件将z表示成x、y的函数，即z=(a^2-2xy)/2(x+y)，再把它带入V=xyz可得V的表达式（略），只与xy有关的无条件极值。

但在很多情形下，将条件极值化为无条件极值并不这样简单。拉格朗日乘数法可直接寻求条件极值，不必先把问题转化到无条件极值的问题。

二、拉格朗日乘数法

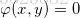要找函数在附加条件下的可能极值点，可以先做拉格朗日函数

其中λ为参数（称为拉格朗日乘子）。求其对x与y的一阶偏导数，并使之为0，然后与附加条件联立，得到如下方程组：

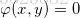由此解出x、y、λ，这样得到的(x,y)就是函数在附加条件下的可能极值点。

此方法还可以推广到多自变量多于两个而条件多于一个的情形，如对于4自变量，2条件的要求，即函数

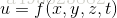
在附加条件

下的极值，可以先做拉格朗日函数

其中λ、μ均为拉格朗日乘子，求其各一阶偏导数，并使之为0，并将其与附加条件联立方程组，可解得可能极值点。

更一般的表达式详见百度百科等。

三、方法推导

寻求函数在附加条件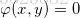下去的极值的必要条件。

如果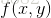在取得极值，那么首先有。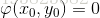

假定在的某一邻域内与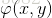均有连续一阶偏导数，且有，由隐函数存在定理1可知，根据附加条件确定的方程可以确定一个连续且具有连续倒数的函数，带入z得

于是在取得极值等价于在取得极值，即有：

而根据隐函数求导公式，由附加条件可得

前两式联立可得

那么上式加上附加条件，即为取极值的必要条件，设，上述必要条件变为以下方程组

若引进辅助函数

那么方程组前两式就是

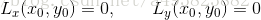
函数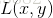称为拉格朗日函数，参数λ称为拉格朗日乘子。

（隐函数存在定理1：条件如定理中所示，对于方程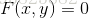，求其全导数

即得

)

四、应用实例

例：求函数在附加条件

下的极值

解：做拉格朗日函数

那么有如下方程组

与附加条件联立（求解过程略）便得。带入得极小值为。