微分方程组解 Stuttering Poisson分布（离散型复合Poisson分布）密度函数的讨论

下载地址https://bbs.pinggu.org/thread-1523398-1-1.html

或http://www.docin.com/p-439526949.html

或http://www.cnki.com.cn/Article/CJFDTOTAL-GDHS201204001.htm

       Poisson分布具有平稳性、独立增量性（无后效性）、普通性。其中的普通性值得我们去思考，例如李贤平所著的《概率论基础》中普通性是这样定义的：在充分小的时间间隔中最多来到一个呼叫。这里的“来到一个呼叫”可以换成其它事件。 把Poisson分布的普通性修改后得到一种推广的Poisson分布—Stuttering Poisson分布，它具有在充分短的时间段内来到多次事件的性质，它在库存管理、运筹学、精算、经济学等领域都有应用。Stuttering Poisson 分布是离散型的复合Poisson 分布，它具有在充分短时间内来到多次事件的性质（叠加性）。例如：来到一个人、来到一个微生物、一封信。那么我们是否可以假设在充分小的时间间隔中最多来到多个人或者多个微生物。结合实际，有：
      情形 1：平信投到邮筒，如果瞬间在那个人投一封信到邮筒，那么形成一个泊松过程,但是每一个人但是可能拿着至少一封邮件,那么单位时间内寄出的信件服从什么分布呢？
      情形 2：显微镜下观察某区域中的细菌时，某些细菌会处于在二分裂繁殖、三分裂繁殖或者多分裂繁殖的过程中，观察到的一个细胞可能是2 个细菌或者更多的细菌。
      情形 3.在罪犯之中，有的人可能是犯有多重谋杀罪。
      情形 4.在保险业中，索赔的客户可能买了多份相同的保险（可以证明，在非寿险精算中常用的负二项分布就是Stuttering Poisson分布）。
      情形 5：学生进食堂吃饭时，我们考虑通过食堂门口的人数（规定一条线作为标志），在食堂门口，我们可以经常看见手牵手并行的伴侣，或者其他朋友关系。
      情形 6：我们考虑人行道上通过桥头的人数（规定一条线作为标志）。在熙熙攘攘的人行道上，有些人是结伴的，他们走在一条线上，两个人结伴并行的，他们可能是一对伴侣，或者其他朋友关系；三个人结伴并行的，他们可能是一家三口，又或者其他原因并行； 在计数的时候，我们的肉眼就难以区分是谁先通过桥头了，于是把并行的当作“合体”来看待。我们假设人结伴通过桥头在整个人群中是有一定比例的。
     情形 7：在库存管理理论中，顾客的到来后，可能一次购买多件相同的商品。

     下面是Stuttering Poisson分布准确数学定义

        萨尔斯伯格（David Salsburg ）的 女士品茶：20世纪统计怎样变革了科学（The Lady Tasting Tea How Statistics Rvolutionized Science in theTwentieth Century）的第28章 电脑随心所欲 注释有提到这种分布:
------------------------------------------------------------------------------------------------------------------------------
统计模型的胜利
       运算密集法在标准工程实践中的扩展，是20世纪末统计革命已经渗透到科学界各个角落的一个实例。数理统计学家们已经不再是统计方法发展唯一的、甚至已经算不上是最重要的参与者了。在过去的70年中，科学家和工程师们并不知道那些刊载于他们期刊中最重要的理论经常一次次地被重新发现[3]。
       有时，应用者应用基础定理时没有进行重新论证，仅仅凭直觉上以为是对的就假定它是正确的。还有的情况是，使用者使用了已经被证明是错误的定理，仅仅是因为这些定理直观上看起来是正确的。存在这种问题的原因，是因为在现代科学教育中概率分布的概念已经根深蒂固，以至于统计学家和工程师们思考问题的方式也是基于概率分布的角度。一百多年前，K·皮尔逊认为，所有的观测都来自于概率分布，而科学的目的就在于估计这些分布的参数。在这之前，科学界相信宇宙遵守着某些规律，如牛顿运动定律，而观测到的任何差异都是因为误差的存在。逐渐地，皮尔逊的观点占据了优势，其结果，每个在20世纪接受科学方法训练的人都理所当然地接受了皮尔逊的观点。这种观点深深地植根于现代数据分析的科学方法之中，几乎没有人去考虑其所以然。很多科学家和工程师使用这些方法，但从不考虑K·皮尔逊观点的哲学含义。
      然而，当科学研究的真正“主体”是概率分布这一观念被广为接受时，哲学家和数学家发现了许多严重的基本问题，我已经在以上的章节中概略地列举了一些，在下一章节将详细论述。
     [3]我在我的博士论文中，使用了一种众所周知的、至少统计学家们都称之为“复合泊松分布”（compound-Poisson distribution）的分布。当我写论文时我必须去查相关的资料，结果我发现了在经济学、运筹学、电子工程以及社会学中都有同样的分布。有些地方它被称为“结巴泊松”（stuttering Poisson）或泊松二项分布（Poisson-binomial）。在一篇论文中，它还被称为“第五街公共汽车分布”（Fifth Avenue bus distribution）。
------------------------------------------------------------------------------------------------------------------------------       笔者根据这个注释，及相关文献，对Stuttering Poisson分布有了更进一步的了解，然后写了一篇论文《微分方程组解 Stuttering Poisson分布密度函数的讨论》（下载地址http://www.docin.com/p-439526949.html）。不知道看过这女士品茶的同志还记得这种分布咩。
       下图证明了在非寿险精算中常用的负二项分布就是Stuttering Poisson分布

      

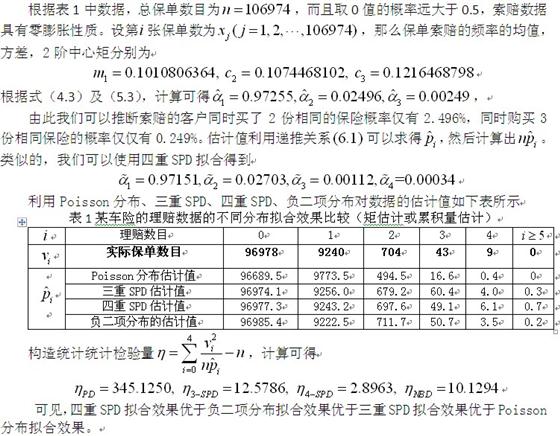
      下面是根据某车险的理赔数据（下文表1中某车险的理赔数据来源于文献[杨静平.非寿险精算[M].北京：北京大学出版社，2006.]）利用Stuttering Poisson分布进行拟合，并与其他一些分布拟合效果进行比较。