如果动态优化问题是处理离散时间with Finite Horizon, 那么解决办法与静态相同。 可是， 当问题推广到 Infinite Horizon 的情形， 大家需要注意 Transversality Condition (TVC). 下面我将慢慢引入 TVC 这概念及其经济含义。

考虑一个经典的吃蛋糕问题 (Cake Eating Problem)

[吃蛋糕问题] 假定在时间 t=0, 你拥有一只蛋糕。你准备靠它度过一生 (from t=0 to t=T). 如果你在时间 t 消费 块蛋糕, 你得到的效用从时间零看等于: 这里 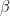在 0 到 1 之间. 即你这辈子的总效用可以被表达为:

请问你应该怎样吃才能使效用极大化?

[分析] 用 记录在时间 t 初始还剩下的蛋糕. 根据定义: . 限制条件可被表示为:

……


……

除了上述显性限制外，还有隐性限制： 和 for any t. 稍作思考，我们知道这些限制中，除了 是”binding”外, 其它都是”nonbinding constraints”。所以我们得加上这个”binding constraint”:

现在，让我们写下Lagragian:

…

…

一阶条件 (First Order Conditions or FOCs)

, t=0, 1, 2, …, T

, t=0, 1, 2, …, T

列出complementary slackness conditions:

……

……

下面来解上述方程及不等式。 首先(3.2) 可推出 for any t, 所以(3.7)说明：
, t=0, 1, 2, …, T

其次，结合(3.4)和(3.9)导出：

当T 取有限值时 （即 Finite Horizon），(3.11) 推出, 即死之前吃光所有的蛋糕。当T 取无限值时（即当你长生不老），的自然推广似乎应当是. 值得注意的是：虽然在吃蛋糕这个问题中，这个推广是对的， 但并非永远是正确的优化必要条件。正确的必要条件是(3.11)的自然推广:

(3.12)便是所谓的Transversality Condition (TVC) under infinite horizon. 在经济增长的模型中可能就不成立， 而 TVC 则是成立的。其经济含义我下面将有评论。

再者， （3.2）（3.3）可导出：

, t=0, 1, 2, …, T

最后，利用(3.13)解 (3.10)同时注意到 和 :

t=0, 1, 2, …, T

[评论]

1. 可能有同学注意到我在 前乘上了 . 这是合法的。乘的数越小，则 越大而已。这里我们乘上了 是为了使 FOCs 看上去更整齐。 同时， 的经济含义也很清晰： current-value shadow price, current-value marginal utility. 被称为 present value shadow price.
   
2. 这里， 称作 discount factor. 说明下一期消费所带来的效用从这期来看需要打个折扣。
   
3. 如果将 当作资本存量(capital stock), 将 当作消费 (consumption), 则我们上面分析的就是最简单的宏观经济模型。这里生产函数就是：. 资本积累方程就是：.
   
4. 注意到 是影子价格，那么TVC 的含义就是最优化要求 资本存量的价值 随着时间的推移趋向于零。若它趋向于某个正数，则说明储蓄过多。
   
5. 其实吃蛋糕的问题有更简单的解法。我们在上面写限制条件时采用的是流量的形式。之所以采用这种形式是因为它便于推广到一般情形。更重要的原因是我想以这种方式引入TVC 的概念。限制条件的另一种写法是：

这是以Present Value 的形式来写的。左边是 present value of life-time consumption, 右边是 present value of life-time resources. 有同学可能会问，既是present value, 为何不见interest rate? 答案是这里利率为零 （资本边际产出为零： 同时折旧率也假设为零）。

[习题] 让成无穷大. 请使用TVC 及FOCs 解出, t=0, 1, 2, …,