R in action读书笔记（19）第十四章主成分和因子分析

jpld

2484

收藏 2015-05-08

第十四章：主成分和因子分析

主成分分析（PCA）是一种数据降维技巧，它能将大量相关变量转化为一组很少的不相关变量，这些无关变量称为主成分。探索性因子分析（EFA）是一系列用来发现一组变量的潜在结构的方法。它通过寻找一组更小的、潜在的或隐藏的结构来解释已观测到的、显式的变量间的关系。

PCA与EFA模型间的区别

主成分（PC1和PC2）是观测变量（X1到X5）的线性组合。形成线性组合的权重都是通过最大化各主成分所解释的方差来获得，同时还要保证个主成分间不相关。相反，因子（F1和F2）被当做是观测变量的结构基础或“原因”，而不是它们的线性组合。代表观测变量方差的误差（e1到e5）无法用因子来解释。图中的圆圈表示因子和误差无法直接观测，但是可通过变量间的相互关系推导得到

14.1 R 中的主成分和因子分析

psych包中有用的因子分析函数

principal()	含多种可选的方差旋转方法的主成分分析
fa()	可用主轴、最小残差、加权最小平方或最大似然法估计的因子分析
fa.parallel()	含平行分析的碎石图
factor.plot()	绘制因子分析或主成分分析的结果
fa.diagram()	绘制因子分析或主成分的载荷矩阵
scree()	因子分析和主成分分析的碎石图

最常见的步骤:

(1) 数据预处理。PCA和EFA都根据观测变量间的相关性来推导结果。用户可以输入原始数据矩阵或者相关系数矩阵到principal()和fa()函数中。若输入初始数据，相关系数矩阵将会被自动计算，在计算前请确保数据中没有缺失值。

(2) 选择因子模型。判断是PCA（数据降维）还是EFA（发现潜在结构）更符合你的研究目标。如果选择EFA方法，你还需要选择一种估计因子模型的方法（如最大似然估计）。

(3) 判断要选择的主成分/因子数目。

(4) 选择主成分/因子。

(5) 旋转主成分/因子。

(6) 解释结果。

(7) 计算主成分或因子得分。

14.2 主成分分析

PCA的目标是用一组较少的不相关变量代替大量相关变量，同时尽可能保留初始变量的信息，这些推导所得的变量称为主成分，它们是观测变量的线性组合。如第一主成分为：PC1=a1X1+a2X 2+……+ak Xk它是k个观测变量的加权组合，对初始变量集的方差解释性最大。第二主成分也是初始变量的线性组合，对方差的解释性排第二，同时与第一主成分正交（不相关）。后面每一个主成分都最大化它对方差的解释程度，同时与之前所有的主成分都正交。数据集USJudgeRatings为例，数据框包含43个观测，12个变量。

14.2.1 判断主成分的个数

判断PCA中需要多少个主成分的准则：

根据先验经验和理论知识判断主成分数；

根据要解释变量方差的积累值的阈值来判断需要的主成分数；

通过检查变量间k × k的相关系数矩阵来判断保留的主成分数。

利用fa.parallel()函数，可以同时对三种特征值判别准则进行评价

> fa.parallel(USJudgeRatings[,-1],fa="PC",n.iter=100,

+ show.legend=FALSE,

+ main="Scree plotwith parallel analysis")

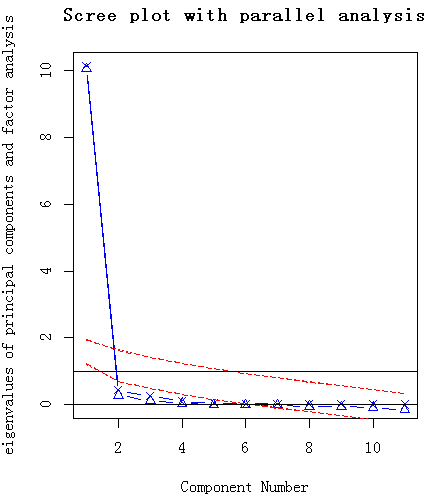
评价美国法官评分中要保留的主成分个数。碎石图（直线与x符号）、特征值大于1准则（水平线）和100次模拟的平行分析（虚线）都表明保留一个主成分即可。三种准则表明选择一个主成分即可保留数据集的大部分信息

14.2.2 提取主成分

principal()函数可以根据原始数据矩阵或者相关系数矩阵做主成分分析。格式为：principal（r,nfactors=,rotate=,scores=）

r是相关系数矩阵或原始数据矩阵；

nfactors设定主成分数（默认为1）；

rotate指定旋转的方法[默认最大方差旋转（varimax）

scores设定是否需要计算主成分得分（默认不需要）。

> pc<-principal(USJudgeRatings[,-1],nfactors=1)

> pc

由于PCA只对相关系数矩阵进行分析，在获取主成分前，原始数据将会被自动转换为相关系数矩阵。PC1栏包含了成分载荷，指观测变量与主成分的相关系数。如果提取不止一个主成分，那么还将会有PC2、PC3等栏。成分载荷（component loadings）可用来解释主成分的含义。此处可以看到，第一主成分（PC1）与每个变量都高度相关，也就是说，它是一个可用来进行一般性评价的维度。

h2栏指成分公因子方差——主成分对每个变量的方差解释度。u2栏指成分唯一性——方差无法被主成分解释的比例.如，体能（PHYS）80%的方差都可用第一主成分来解释，20%不能。相比而言，PHYS是用第一主成分表示性最差的变量。SS loadings行包含了与主成分相关联的特征值，指的是与特定主成分相关联的标准化后的方差值（本例中，第一主成分的值为10）。最后，Proportion Var行表示的是每个主成分对整个数据集的解释程度。此处可以看到，第一主成分解释了11个变量92%的方差。

14.2.3 主成分旋转

旋转是一系列将成分载荷阵变得更容易解释的数学方法，它们尽可能地对成分去噪。旋转方

法有两种：使选择的成分保持不相关（正交旋转），和让它们变得相关（斜交旋转）。旋转方法也会依据去噪定义的不同而不同。最流行的正交旋转是方差极大旋转，它试图对载荷阵的列进行去噪，使得每个成分只是由一组有限的变量来解释（即载荷阵每列只有少数几个很大的载荷，其他都是很小的载荷）。

方差极大旋转的主成分分析

>rc<-principal(Harman23.cor$cov,nfactors=2,rotate="varimax")

> rc

观察RC1栏的载荷，你可以发现第一主成分主要由前四个变量来解释（长度变量）。RC2栏的载荷表示第二主成分主要由变量5到变量8来解释（容量变量），两个主成分旋转后的累积方差解释性没有变化（81%），变的只是各个主成分对方差的解释度（成分1从58%变为44%，成分2从22%变为37%）。各成分的方差解释度趋同，准确来说，此时应该称它们为成分而不是主成分（因为单个主成分方差最大化性质没有保留）。

14.2.4 获取主成分得分

从原始数据中获取成分得分

> library(psych)

> pc<-principal(USJudgeRatings[,-1],nfactors=1,score=TRUE)

> head(pc$scores)

当scores = TRUE时，主成分得分存储在principal()函数返回对象的scores元素中。

还可以获得律师与法官的接触频数与法官评分间的相关系数：

> cor(USJudgeRatings$CONT,pc$score)

PC1

[1,] -0.008815895

律师与法官的熟稔度与律师的评分毫无关联

获取主成分得分的系数

> library(psych)

>rc<-principal(Harman23.cor$cov,nfactors=2,rotate="varimax")

> round(unclass(rc$weights),2)

主成分得分：

PC1=0.25*height+0.3*arm.span+0.3*forearm+0.29*lower.leg-0.06*weight-0.08*bitro.diameter-0.1*chest.girth-0.04*chest.width

14.3 探索性因子分析

EFA的目标是通过发掘隐藏在数据下的一组较少的、更为基本的无法观测的变量，来解释一组可观测变量的相关性。这些虚拟的、无法观测的变量称作因子。（每个因子被认为可解释多个观测变量间共有的方差，因此准确来说，它们应该称作公共因子。）模型的形式为：

其中Xi是第i个可观测变量（i = 1…k），Fj是公共因子（j = 1…p），并且p<k。Ui是Xi变量独有的部分（无法被公共因子解释）。ai可认为是每个因子对复合而成的可观测变量的贡献值。

> options(digits=2)

> covariances<-ability.cov$cov

> correlations<-cov2cor(covariances)

> correlations

14.3.1 判断需提取的公共因子数

用fa.parallel()函数可判断需提取的因子数：

> library(psych)

> covariances<-ability.cov$cov

> correlations<-cov2cor(covariances)

> fa.parallel(correlations,n.obs=112,fa="both",n.iter=100,

+ main="Screeplots with parrallel analysis")

判断心理学测验需要保留的因子数。图中同时展示了PCA和EFA的结果。PCA结果建议提取一个或者两个成分，EFA建议提取两个因子

14.3.2 提取公共因子

决定提取两个因子，可以使用fa()函数获得相应的结果。fa()函数的格式如下：fa(r,nfactors=,n.obs=,rotate=,scores=,fm=)

r是相关系数矩阵或者原始数据矩阵；

nfactors设定提取的因子数（默认为1）；

n.obs是观测数（输入相关系数矩阵时需要填写）；

rotate设定旋转的方法（默认互变异数最小法）；

scores设定是否计算因子得分（默认不计算）；

fm设定因子化方法（默认极小残差法）。

与PCA不同，提取公共因子的方法很多，包括最大似然法（ml）、主轴迭代法（pa）、加权最小二乘法（wls）、广义加权最小二乘法（gls）和最小残差法（minres）未旋转的主轴迭代因子法:

> fa<-fa(correlations,nfactors=2,rotate="none",fm="pa")

> fa

两个因子解释了六个心理学测验60%的方差。不过因子载荷阵的意义并不太好解释，此时使用因子旋转将有助于因子的解释。

14.3.3 因子旋转

用正交旋转提取因子

> fa.varimax<-fa(correlations,nfactors=2,rotate="varimax",fm="pa")

> fa.varimax

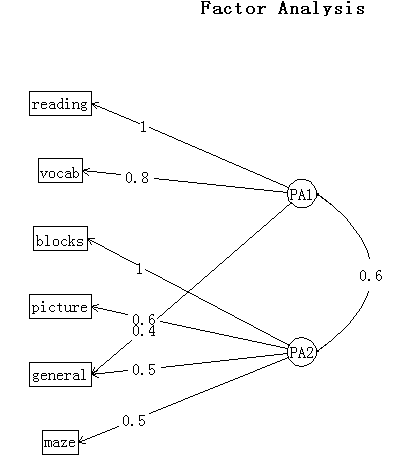
结果显示因子变得更好解释了。阅读和词汇在第一因子上载荷较大，画图、积木图案和迷宫在第二因子上载荷较大，非语言的普通智力测量在两个因子上载荷较为平均，这表明存在一个语言智力因子和一个非语言智力因子。

用斜交旋转提取因子:

> fa.promax<-fa(correlations,nfactors=2,rotate="promax",fm="pa")

> fa.promax

根据以上结果，你可以看出正交旋转和斜交旋转的不同之处。对于正交旋转，因子分析的重点在于因子结构矩阵（变量与因子的相关系数），而对于斜交旋转，因子分析会考虑三个矩阵：因子结构矩阵、因子模式矩阵和因子关联矩阵。因子模式矩阵即标准化的回归系数矩阵。它列出了因子预测变量的权重。因子关联矩阵即因子相关系数矩阵。factor.plot()或fa.diagram()函数，你可以绘制正交或者斜交结果的图形。