全部版块 我的主页
› 论坛 › 经济学论坛 三区 › 马克思主义经济学
谈公平——从数学角度严密证明资本家该拿大头
nofear
24846 198
2008-10-24

这是转贴。

昨天在设计游戏中宠物雌雄比例的时候（关系到生育），我提到，雌雄比例只要差一点点，价格就会差很多。然后我找了这篇文章给我边上数学硕士出身的同事看。她一看就说，这篇文章她找了好久了。其实这篇文章，我也看过很多遍了，经典！

我觉得这篇文章，值得广为转载。

原文出处：http://episte.math.ntu.edu.tw/articles/mm/mm_16_3_08/index.html

談公平

楊照崑
      

 
 


前言

「員工拼死幹活，老闆毫無表示，員工創造利潤，有權要求分享$\cdots\cdots$」這是黃凡近著，〈財閥〉長篇小說中工人向資本家要求公平待遇的口號。生動的刻劃出了一些社會上的不平之鳴。「不平」，不但受害人覺得委曲，就是旁觀者也憤怒難忍，仁者悲天憫人，奔走呼號，勇者路見不平，拔刀相助，而對一個求智者而言，我們能不能客觀的決定怎樣才是公平？是資本家剝削得太厲害，還是勞工要求過份？您也許不會相信一個簡單的數學公式就可以基本上瞭解這個問題，而且讓我們看到一幅嶄新的圖畫，體會到人間的真理。

有人說過問題是數學的靈魂。那麼我們就從問題開始吧。假定有一個資本家（廠主）、一個工程師及二個工人。資本家有工廠，但若沒有工程師及工人則不能賺錢。若資本家與工程師合作，沒有工人，則二人大才小用，做些工人的工作，每月可賺三萬元，若加一個工人，因工人有體力技術，效率大增，三人合作每月可賺6萬元，若再加一工人，則一月可賺9萬元。但若只有廠主與工人沒有工程師，則工廠亦不能開工。現在問這9萬元的利潤要如何分配方為公平合理？（請注意這九萬元完全是利潤，工廠保養、資金利息、股東紅利均已扣除。）

廠主可能對工人說：我們二一添作五，一個月給你一萬五吧。

工人可能會回答，這豈不是太黑。我們每人每月為工廠「淨」賺三萬。給我們一人二萬有何不可？這樣你們仍可以白白分到我們勞工所創的二萬利潤。何必貪得無厭。

廠主會說：笑話，我不給你工作，別說一萬五，你一毛都賺不到，給你一萬五還人心不足！於是紛爭遂起，工說工有理，主說主有理。那麼聰明的你會站在那一邊呢？我們能用理智來解決這個分配問題嗎？在往下看之前，我希望您暫時合起本文，閉眼想一想這個問題應如何著手解決。先自己想清楚再看答案是增加數學趣味及功力的重要法則。

想好了？那麼我先告訴您答案，一個相當公平的分配應是廠主與工程師各得三萬五，二個工人各得一萬元。不公平？不，再找不到比這公平的法則了。

在談到數學之前，我們可以看看這個問題的博大精深。幾乎所有的經濟問題都與這個問題有關。醫院賺大錢，醫生、護士、技師、警衛均不可少，他們要如何分配這筆大錢？學校中校長、教員、職員、工友在待遇上應有何差別？學生論文發表，教授的功勞應算多少？更進一步，我們身為社會一份子，應付多少稅，取多少薪水，也可做如是觀。一切權利的基礎也應從公平上著手，我不虧待人，但我也不允許別人虧待我。

謝卜勒 (Shapley) 公平三原則

首先我們必須明白有合作才有分配公不公平的問題。否則你走你的陽關道打獵，我過我的獨木橋捕魚，在山吃山，靠水吃水，各顧自己，就談不到分配不均的問題。今令 ω 為一個可由多人合作的工作，而 S 表示可以參與工作的人們的集合。若 U 為 S 的一個子集，則 $\omega(U)$ 表示 U 人合作時可得的工作利潤。以前面工廠為例，則

\begin{displaymath}<br>S = \{ \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \ch...<br>...0.1pt{\fontfamily{cwM3}\fontseries{m}\selectfont \char 14}} \}<br>\end{displaymath}
 


若 U={廠主, 工程師} 時，$\omega(U)=3$(萬元)，若 U={廠主, 工程師, 工人甲}，則 $\omega(U)=6$，若 U={廠主, 工人甲}，則 $\omega(U)=0$，為了簡便起見，令 S 中的元素以 1,2,…,n 為代號，即 $S = \{1,\cdots,n\}$。令 $\phi(\omega)$ 表示 i 成員在 ω 工作上該得的報酬。謝卜勒在1953年的論文中，訂下了三個公平的原則。

原則1：報酬與名字無關，只與各人的貢獻有關。即若 i 與 j 互換而不影響 ω 時， $\phi_{i}(\omega)=\phi_{j}(\omega)$。

沒有人會反對這個原則，即同工應同酬，張三若可做李四的事，則張三可拿李四的報酬，與他叫張三或李四無關。

原則2：利潤屬於工作者， $\sum_{i\in U} \phi_{i}(\omega)=\omega(U)$ 對所有 $U\subset S$均成立。

這也是一個公平的原則，U 人合得的利益，自然分給 U 裡的人。

原則3：若有二件工作 $\omega_1$ 與 $\omega_2$，則 $\phi_i (\omega_1,\omega_2)$ = $\phi_i (\omega_1) + \phi_i (\omega_2)$ 對所有 i 均成立。

這也是無人反對的公理，我做二份工作，自可得二分酬勞。

稀奇的是(在謝氏原論文中，他亦稱奇)。只要這三個原則，即可求出 $\phi_i(\omega)$。

定理（Shapley）：根據上項三原則，若對所有 $U\subset S,\omega(U)$ 已給定，則 $\phi_i(\omega)$ 的唯一解為

\begin{displaymath}<br>\phi_i (\omega) = \sum_{ U \subseteq S} r_n (s)<br>[\omega(U)-\omega(U-\{i\})] \eqno{(1)}<br>\end{displaymath}
   

s = U 所含之元素數目,
$r_n = \frac{(s-1)!(n-s)!}{n!}$
    
且 U-{i} 表示 U 中減去成員 {i}。

雖然本定理的證明不長(大約二頁，高中代數程度)，我們不在此重複，有興趣的讀者一定可以從本文的參考資料中找到。而且下文中會對(1)式做直觀的分析，即使不查證明，多數人也會相信(1)是一個公平的分配方式。為了明瞭此公式的用法，讓我們演算一下廠主的報酬，令

S={1,2,3,4}


1,2,3,4 依次代表廠主，工程師，工人甲乙。U 是 S 的子集合，共有 24=16 個。可細列如下：

(1) 空集合及含有一個元素的集合均使 $\omega(U)-\omega(U-\{i\})=0-0=0$。

(2)含有二個元素的集合有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)。其中只有 $\omega(1,2)-\omega(2)=3-0=3$，其餘均為0，而

\begin{displaymath}<br>r_2=\frac{(2-1)!(4-2)!}{4!}=\frac{1}{12}\mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 1}}<br>\end{displaymath}
   

(3)含有三個元素的集合有(1,2,3),(1,2,4),(1,3,4),(2,3,4)，其中

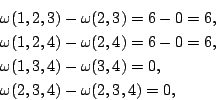
\begin{eqnarray*}<br>&& \omega(1,2,3) - \omega(2,3)=6-0=6,\&& \omega(1,2,4) - \o...<br>...a(1,3,4) - \omega(3,4)=0,\&& \omega(2,3,4) - \omega(2,3,4)=0,<br>\end{eqnarray*}
   


且

\begin{displaymath}<br>r_3=\frac{(3-1)!(4-3)!}{4!}=\frac{1}{12}<br>\end{displaymath}
   

(4)含有四個元素的集只有(1,2,3,4)得

\begin{displaymath}<br>\omega(1,2,3,4)-\omega(2,3,4)<br>=9-0=9,\mbox{ {\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}}r_4=\frac{1}{4} \; .<br>\end{displaymath}
   

因此求得

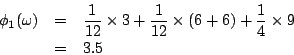
\begin{eqnarray*}<br>\phi_{1}(\omega) &=& \frac{1}{12} \times 3 + \frac{1}{12} \times<br>(6+6) + \frac{1}{4} \times 9 \&=& 3.5<br>\end{eqnarray*}
   


同理可得

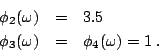
\begin{eqnarray*}<br>\phi_2(\omega) &=& 3.5 \\phi_3(\omega) &=& \phi_4(\omega)=1 \; .<br>\end{eqnarray*}
   


現在如果誰要再說這種分配不公平就為時已晚了，因為一旦你承認了謝卜勒三原則，則剩下的推導全是推不倒，像 a+b=b+a 之類的數學公理。而謝卜勒原則似乎又無懈可擊。因此我們不得不承認這個 3.5:3.5:1:1 是一個公平的分配法。

從另一個角度來看(1)式，我們發現

\begin{displaymath}<br>\omega(U)-\omega(U-\{i\})<br>\end{displaymath}
 


表示的是 {i} 加入 U 時所增加的(邊際)利潤，也就是 {i} 所帶給 U 的利潤。而 rn(s) 表示在所有 1,2,…,n 排列中，{i} 在 s 位置而能保持前後成員不變的或然率，因 s 是 U 所含的元素數目，也就是 {i} 成為 U 中最後加入成員的或然率。因此(1)所表示的是 {i} 成員為 S 團體帶來邊際利潤的期望值，這自然應是 {i} 所得到的報酬。好像不容易說得清楚，且看一個例子。因前例 4!=24 太大了一點，我們在前例中減少一個工人，看看(1)的分配是什麼回事。同時也可以比較一下少一個工人時對各人收入的影響。現在 S={1,2,3} 依次代表了廠主、工程師，及工人甲。表一的左邊有這三個數的全部排列法。其第二，三，四列代表的是在這種排列下，各人所帶的邊際利潤。以第一行的排列 1 2 3 為例。廠主先到，他不能開工，因此他帶來的利潤是 0，工程師第二個到，他與廠主合作可得 3 萬利潤，因此他帶來的邊際利潤是 3(不全是他的功勞，但算他帶來的)，工人最後來，他又帶來了 3 萬利潤 因此這 3 萬就記在工人名下，因此在第一行中各人所帶來的利潤是 0,3,3，但我們沒有理由讓廠主先到，這 3! 的排列應有同等的機會(很公平是不是？)因此一平均下來，各人所帶來的利潤，也就是他們應有的報酬是 2.5,2.5,1。表一的最後三列是代表此表與(1)式的關係，只要仔細對照一下，就可以看出(1)所表示的就是這些排列下所產生的平均值。

排列123含1的 Us$\gamma_n(s)$
123033{1}  
132060{1}12/6
213303{2,1}21/6
312060{3,1}21/6
231600{1,2,3}  
321600{1,2,3}32/6
和15156  1
平均 (和/6)2.52.51   

表一：對 {i} 而言的邊際利潤

若把表一的結果與先前有二個工人的結果比較，我們會發現多來的工人乙與原先的工人甲同工同酬(很合理，是不是？)，都得了一萬元的報酬，但他所造成的另外二萬利潤則又被廠與工程師吞去了 (您覺得工人很倒霉是不是？還有更倒霉的事情在後面，如果真的要公平的話。) 因此無論由三原則推導，或由(1)式直觀，我們發現公平的分配並不像我們想像的那麼難纏。謝卜勒能看到這一點已造成他成為一代宗師的地位，他的公式已成為數理經濟學的柱石。

謝氏定理一些有趣的結果

工作不能增加利潤，則他的報酬當是 0。此人稱為冗員 (dummy)，因對一個冗員 i 而言， $\omega(U)-\omega(U-\{i\})$ 恆為 0，故 $\phi_{i}(\omega)=0$。

在上題中我們看到工程師與廠主的報酬相同，這似乎與事實不合，在大部分的工廠中，工程師拿不到廠主的待遇。這個原因是在一般情形下，工程師不只一個，尤其當工程師供過於求時，他們的身價就會慘跌。現設 S={廠主，工程師甲，工程師乙，工人甲} 其代號仍依次為 1,2,3,4。但只需一個工程師就夠了。在這時候，若廠主請了其中的一位，他仍付他二萬五？且看公式(1)中 $\phi_{2}(\omega)$ 的結果。

(1) 對空集合及含一元素之集合而言， $\omega(U)-\omega(U-\{2\})=0$。

(2) 對二元素的集合而言，只有 $\omega(1,2)-\omega(1)=3$不為0。

(3) 對三元素的集合而言，只有 $\omega(1,2,4)-\omega(1,4)=6$ 不為 0 ( U(1,2,3)-U(1,3)=3-3=0，因另一個工程師乙捷足先登，工程師甲的工作就泡了湯。)

(4) 對四元素之集合 $\omega(1,2,3,4)-\omega(1,3,4)=6-6=0$。因此工程師甲的報酬應為 $\frac{3}{12}+\frac{6}{12} =0.75$。引用原則一，或再導一次可知工程師乙之公平所得亦為0.75，二者之和只有1.5萬，竟然比原來一個人可得的2.5萬少了一萬。這說明了供過於求一個可怕的結果，多一個工程師不但不能增加工程師的收入，而且拖了同仁下水。其原因自然因為廠主有恃無恐，不怕找不到工程師而可以加以殺價的緣故。但這個事實竟能從公平三原則中反映出來，不可不謂數學的奇蹟。現在看看資本家與工人可因此多獲利多少。稍加計算可得 $\phi_1(\omega)=3.25$, $\phi_4(\omega)=1.25$，可見其中大部分的好處為廠主所得，但工人也因工程師多而身價小增。依理往前推，若工程師再多，則其身價必又再跌，原來工程師之所以可以與資本家平分秋色乃是因工程師只有一位，沒有他開不了工，奇貨可居之故。當然若只有一個工程師而有二個工廠，則他的身價會增加而廠主的報酬就要下跌。但在一般社會中都是資本家少，工程師多，而勞工更多，因此工人可以分得之公平工資之慘，可以想見。

公式(1)之推導固然精彩，可惜(幸好)在一般情形下，不容易計算，因為 $U \subseteq S$ 含有 S 中全部的子集，有 2n 個。當 n 稍大時，計算量就會壓死計算機。但在某些情形下，特別是成員的能力大多相同時，表一中的排列法就能減少到可以計算的地步。現舉一個這樣的例子。

設某鳥商請一個村子裡的人為他養鳥，各家養一隻。到收購的時候，他宣佈他只能買成對的鳥兒，一對一千元。村人各戶人家集合算了一下，發現有雄鳥110隻，雌鳥90隻，因此可賣九萬元，為了不使養雄鳥之家搶賣打破頭起見，全村一氣，算大家共賣，因此得了九萬元，放生了20隻雄鳥。現在問題是錢要如何分配才「公平」。當養雄鳥之家主張均攤，即每隻鳥值 9萬/200 = 450 元，但養雌鳥人家認為物以稀為貴，雌鳥之所以活得少，必定是比較難養，理應多分一點，紛爭又起，如何擺平？如果我們以謝卜勒原則看公平，則因鳥只有二種，可以求出

\begin{displaymath}<br>\phi_{i}(\omega)=\sum_{k=1}^{n-1}r_n(k+1)\sum_{x\geq[\frac{k}{2}+1]}^{k}{n_2 \choose x}{n_1-1 \choose k-x}<br>\eqno{(2)}<br>\end{displaymath}
 


式中 [y] 表 y 之整數值，n1 為 i 所屬之類的鳥數，即若 i 為雄，則n1=110，i 為雌，則 n1=90,n2 另一類鳥數，n=n1+n2。用計算機算出結果是雄鳥單價值 109 元，雌鳥單價為 876 元，而全部雄鳥之值只有雌鳥的 6.5 分之一。其實稍不平衡，價差就很驚人，如果雄、雌各為 102 及 98 隻，則其單價比為 1:1.82，物以稀而貴，一致於此。

記得若干年前臺灣適婚年齡者男多女少，少女身價百倍。現在好像是女多男少，單身漢行情看漲。不過人間的情形很複雜，我們不能把每位少男少女像鳥兒一樣看為等價。因各人條件不同，每個人的公平地位就不容易由(1)計算出來(2n子集而$n\geq10^6$?)，條件好的男女是不介意情敵多少的。但(1)式至少能解釋一個重要的現象，稍不平衡，就產生極大的價差。

其實人們雖不知公式(1)，但這種現象早已深植於人們的心中，每個人都想改變自我環境，使得公式(1)對我有利。當供過於求的時候，人們曾經把糧食、牛奶、羊毛倒入海中以求增加價格，以鳥兒為例，若雄鳥人家先商量好，偷偷放走20隻 則對養雄鳥人家都有利， (若放走30隻則更有利，這時候雌鳥每隻只值201元而雄鳥值773元，雖全部只剩下80對鳥兒，但對雄鳥人家而言則有利。但這要合作才行，若你自己把鳥放了，則可能一文都拿不到。)各行業防止供過於求，用執照、工會、幫會、碼頭等加以限制人數。而大家也都知道要進到一個行業中成為一個不可少的人。

然而也有些人雖不喜歡不平，但卻想破壞公平，有人破壞第一原則，利用各種關係，使得報酬與名字有關，他是我的兒子，報酬就自然加大，有的破壞第二原則，沒有做事的人也巧立名目，拿一些錢。當然，最壞的是鼓勵生產力不足的人用搶，嚴重的破壞了公平的分配。

一點感想

從公平的原則看來，社會上才智高的人似乎反而沒有拿到他份內公平的報酬，這些不可少的創業家，發明家，若照謝卜勒的公式，他們的報酬可能應是不可思議的大。因此當我們未來再為自己訴不平的時候，就該想到公式(1)：從公平的觀點來看，是天下人負我，還是我負天下人？

Shapley 的原文發表在 Shapley,L.S.(1953)〈A value for n-person games〉,in《Contributions to the Theory of Games》, Vol. II,Ed. by H.W. Kubn and A.W. Tucker, Princeton University Press.
一些最近的發展可看

《The Shapley Value:Essays in Honor of Lloyd S. Shapley》,1988,Ed. by A.E. Roth, Combridge University Press.

Shapley 1953年論文亦收在此書內。

[此贴子已经被作者于2008-10-25 16:50:48编辑过]

二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

全部回复
nofear
2008-10-25 16:52:00
自己顶一下。
二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

fujo11
2008-10-25 17:29:00

数学不能证明啥是公平的。

这是标准的垃圾进垃圾出

二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

nofear
2008-10-25 17:48:00
以下是引用fujo11在2008-10-25 17:29:00的发言：

数学不能证明啥是公平的。

这是标准的垃圾进垃圾出

先不要急着下结论。创造这个公式的谢卜勒毕竟也是诺贝尔奖获得者，无论如何也值得一看。

当然，就这样看，的确会看得有点头晕。我简介一下思路。

作者的思路是：

每个人应该获得他加入合作后创造出来的边际利润。

比方说，A一个人能赚1万元，B加入合作后，可以使利润从1万增加到1.5万，那么B带来的边际利润就是5000元，B就该拿5000元。

但是我们不能保证每次都是A先加入合作，然后出现B，也有可能B先出现，然后A加入。那么假设B一个人是一分钱也赚不到的，A加入后，带来的边际利润是1.5万，那么这种情况下，就应该A拿1.5万。

A先出现还是B先出现，我们不知道，我们只知道两种情况都有。他们谁先出现的概率大，我们也不知道，只能假设概率均等。因此，公平的分配方法就是把每个人出现先后都排列出来，然后看每个人每种情况带来的边际利润是多少，然后有多少种排列，就除以多少

比方说，按上面的例子，有两种可能性：

第一种：A先出现，边际利润1万，然后B出现，边际利润5000

第二种：B先出现，边际利润0，然后A出现，边际利润1.5万。

那么公平分配就是B的第一种情况的5000加上第二种情况的0，等于5000，然后除以2（2种情况），B应该拿2500。A第一种情况1万，第二种情况1.5万，加起来2.5万，除以2，等于1.25万。公平的分配，就是A得1.25万，B得2500。

事实上，人的判断虽然没有经过计算，但往往基本符合计算结果。我就试过问一些有领导经验的人，先假设了题目，然后问如何分配，往往和计算结果很接近。

二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

吴本龙
2008-10-25 18:00:00

正宗的垃圾帖

二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

jackloo
2008-10-25 18:43:00

用公平三原则并不能证明分配的公平。

举个反例就可以说明，在你的例子中，如果增加资本家的数量，那么你的证明过程，就会发现资本家的分配会减少，但实际上并没有发生变化，所以你的证明是错误的。

还有你后面回帖的例子中说

“每个人应该获得他加入合作后创造出来的边际利润。”

“比方说，A一个人能赚1万元，B加入合作后，可以使利润从1万增加到1.5万，那么B带来的边际利润就是5000元，B就该拿5000元。”

也不尽然。如果我是资本家，发现B带来的边际利润是5K的话，那我会连A和B的工资也降到5K左右的。我相信所有的资本家都会按照我的想法去做的。

可见，你推论的依据都是一些似是而非的东西，站不住脚。

二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

点击查看更多内容…
相关推荐
栏目导航
热门文章
推荐文章

说点什么

分享

微信QQ空间QQ微博
扫码加好友，拉您进群
各岗位、行业、专业交流群