猫爪 发表于 2009-8-28 22:28 
我也向馒头斑竹请教一个思考很久的问题:
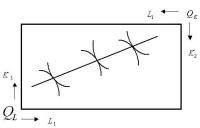
契约曲线其中的一段是否会出现从左上到右下的“扭曲”?
说请教是太客气了,我也不知道这个问题的答案。下面是我的一下简单的推导,大家看看,我也不知道对不对。
考虑这个问题,假设每个人的效用函数分别是
u1(
x,
y),
u2(
x,
y),两种商品的禀赋分别是
wx,
wy,那么契约曲线在内点一定满足

rewrite:
F(
x,
y) =
u1
x(
x,
y)
u2
y(
wx −
x,
wy −
x) −
u1
y(
x,
y)
u2
x(
wx −
x,
wy −
y)
其中
uix是第i个人对商品x的边际效用。因为我们考虑的是扭曲的问题,所以应该只需要讨论内点解。上式定义了一个
y对
x的隐含数,如果这个曲线左上到右下扭曲的话,那么也就是说这个隐含数是递减的。假定这个函数可导(纯粹为了省事,当然可能不可导),那么用隐含数定理可知:


现在我们就可以讨论了:
如果我们要求偏好是单调的且凸的话,那么我们就有

。但我们不知道
uixy的符号,在这种情况下我们没法确定
dy /
dx的符号,那么契约曲线也就有可能递减。如果

,比如Cobb-Douglass,或者任何x y可分离的情况,那么我们可以确定

,这样也就不可能单调递减。除此之外,似乎在这个general form下没有什么办法可以确定dy/dx的符号。
如果我们进一步假定两个人的效用函数相同,那么:
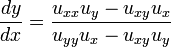
这样的话这个问题就可以有一个确定的答案。如果

,那么如前所述,必有

,不可能出现扭曲;所以我们只需要讨论
uxy < 0。给同样的假定,即凸性和单调性,我们现在有:

这个地方有点不严谨,因为我直接用了海赛阵而没有用加边海赛;结果应该差不多的,就偷懒了:)
这个条件等价于:

这里面不等号变换了方向,因为每一项都是负的。那么,如果在dy/dx那个式子里面的分子大于零,那么一定有分母也大于零;换句话说,上下同号,故我们有

,不可能出现扭曲:

最后这个不等式是这样的推导的:


从分子大于零我们知道:
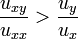
将这个式子带入上式,我们有:

最后这个式子也就等价于分母大于零了。
如果分子小于零的话,根据上面的逻辑,分母也会小于零。所以无论是什么情况,我们都有dy/dx\geq 0,这也就是说,契约曲线不会出现递减情况,也就不会扭曲。
总结一下:
如果两个人的效用函数不相同,那么没有扭曲的充分条件是偏好的凸性,单调性,以及

。我觉的最后这个条件应该是有个名字的,跟complementary 有没有关系?不知道了,那位大哥指导一下。。。。。因为最后这个条件并不是最基本的条件,那么有可能出现左上到右下的扭曲
如果两个人的效用函数相同,那么只要偏好满足凸性和单调性(这点不太严谨,我证明的是效用函数满足凹性和单调性,关于凸性的问题,我觉的应该是可以成立的,不过懒得弄加边海赛了……),那么就不可能出现扭曲的情况。
最后,那位大哥能指导一下怎么在这个论坛输入数学公式啊,我这个可是在wiki里面敲出来然后粘过来的……很痛苦。
update:
似乎公式显示怎么着也有点乱,感兴趣的可以去我的wiki上看一下比较清晰的版本:
http://en.wikipedia.org/wiki/User_talk:Malin84





 。但我们不知道uixy的符号,在这种情况下我们没法确定dy / dx的符号,那么契约曲线也就有可能递减。如果
。但我们不知道uixy的符号,在这种情况下我们没法确定dy / dx的符号,那么契约曲线也就有可能递减。如果 ,比如Cobb-Douglass,或者任何x y可分离的情况,那么我们可以确定
,比如Cobb-Douglass,或者任何x y可分离的情况,那么我们可以确定 ,这样也就不可能单调递减。除此之外,似乎在这个general form下没有什么办法可以确定dy/dx的符号。
,这样也就不可能单调递减。除此之外,似乎在这个general form下没有什么办法可以确定dy/dx的符号。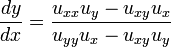
 ,那么如前所述,必有
,那么如前所述,必有 ,不可能出现扭曲;所以我们只需要讨论uxy < 0。给同样的假定,即凸性和单调性,我们现在有:
,不可能出现扭曲;所以我们只需要讨论uxy < 0。给同样的假定,即凸性和单调性,我们现在有:

 ,不可能出现扭曲:
,不可能出现扭曲:


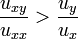

 。我觉的最后这个条件应该是有个名字的,跟complementary 有没有关系?不知道了,那位大哥指导一下。。。。。因为最后这个条件并不是最基本的条件,那么有可能出现左上到右下的扭曲
。我觉的最后这个条件应该是有个名字的,跟complementary 有没有关系?不知道了,那位大哥指导一下。。。。。因为最后这个条件并不是最基本的条件,那么有可能出现左上到右下的扭曲假设在一个价格内生的体系内,两个相同的效用函数下,对于一个效用函数而言,是否可以肯定,不存在某种商品的相对价格下降,同时消费量下降的情况?这是否能够说明,并不是像无常大师所言,竞争消除了吉芬商品;而是,“相同的偏好”这一条件,同时产生了“竞争”和“消除了吉芬商品”这两种后果。
 扫码加好友,拉您进群
扫码加好友,拉您进群




 收藏
收藏

