混合高斯模型（EM-GMM）的应用与实现

混合高斯模型（Expectation-Maximization Gaussian Mixture Model, EM-GMM）是一种强大的概率建模方法，适用于多种随机分布的拟合与分析。其典型应用场景包括新能源领域的风电和光伏发电预测误差建模、聚类任务、异常检测以及生成式建模等。

在实际研究中，尤其是不确定性量化方向，EM-GMM 展现出了极强的适应性和准确性。以下将从应用领域、代码实现、分布图绘制及程序优化四个方面进行详细说明。

1. 应用场景概述

该算法能够处理复杂的多峰分布问题，因此特别适合用于描述具有不确定性的自然现象。例如，在风力发电中，预测误差往往不遵循单一正态分布，而是呈现出多个分布模式的叠加状态；同样地，光伏出力受天气、光照角度等因素影响，其预测偏差也具备类似的复杂结构。利用 EM-GMM 可以有效拟合这些误差的联合分布，为风险评估与调度决策提供统计基础。

此外，该方法还可广泛应用于：

• 聚类分析：无需标签即可对数据进行软划分；
• 异常检测：通过低概率区域识别异常样本；
• 生成模型：基于学习到的分布采样新数据点。

import numpy as np
from sklearn.mixture import GaussianMixture

# 生成一些模拟数据，这里假设是风电预测误差数据
data = np.random.normal(0, 1, 1000)

# 创建一个高斯混合模型，假设这里我们知道是两个高斯分布混合
gmm = GaussianMixture(n_components = 2)

# 对数据进行拟合
gmm.fit(data.reshape(-1, 1))

# 预测每个数据点属于哪个高斯分布
labels = gmm.predict(data.reshape(-1, 1))

2. 核心代码实现

下面展示一段基于 Python 的基础实现流程，用于构建并训练一个混合高斯模型：

导入必要的库：

numpy

sklearn.mixture

GaussianMixture

首先引入 NumPy 作为核心数值运算工具，同时从 scikit-learn 中调用 GaussianMixture 类来实现模型主体功能。

随后生成模拟数据集以演示整个过程：

np.random.normal

这里构造了 1000 个服从均值为 0、标准差为 1 的风电预测误差样本，用以代表真实场景中的预测残差序列。

接下来初始化模型：

创建一个 GaussianMixture 实例，并设定组件数量为 2，即假设数据由两个不同的高斯分布混合而成。这一参数可根据 AIC/BIC 准则或交叉验证结果动态调整。

n_components = 2

使用 fit() 方法对数据进行训练：

gmm.fit

该步骤通过 EM 算法迭代优化模型参数，使整体似然最大化，从而获得最优的分布组合。

最后执行分类预测：

gmm.predict

调用 predict() 获取每个数据点最可能归属的子分布类别，输出结果存储于标签变量中：

labels

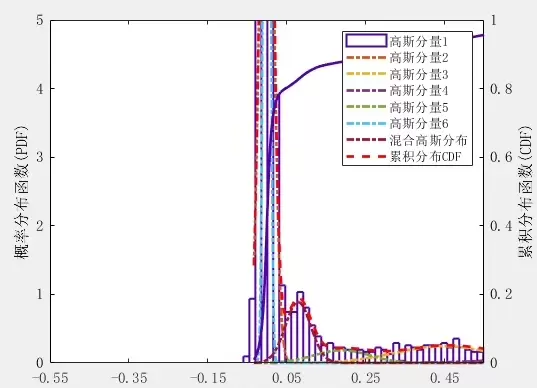
3. 累计分布与逆累计分布计算

为了更深入理解数据的整体分布特征，累计分布函数（CDF）和逆累计分布函数（Inverse CDF）是不可或缺的分析工具。

import matplotlib.pyplot as plt

# 计算累计分布函数
sorted_data = np.sort(data)
cdf = np.arange(1, len(sorted_data) + 1) / len(sorted_data)

# 绘制累计分布图
plt.plot(sorted_data, cdf)
plt.xlabel('Data Value')
plt.ylabel('Cumulative Distribution')
plt.title('CDF of Wind Prediction Error')
plt.show()

# 逆累计分布计算（这里简单示意，实际应用可能更复杂）
def inverse_cdf(cdf_value):
    for i in range(len(cdf)):
        if cdf[i] >= cdf_value:
            return sorted_data[i]
    return sorted_data[-1]

上述代码段展示了如何计算并可视化累计分布：

先对原始数据排序，再计算对应的经验 CDF 值：

cdf

然后借助 matplotlib 绘制曲线图，直观呈现数据累积比例随取值变化的趋势：

matplotlib

对于逆累计分布，设计了一个简单但实用的函数：

inverse_cdf

该函数接收一个概率值（如 0.95），返回对应分位点的数据值，可用于置信区间估计或极端事件分析。在实际工程中，可结合插值技术进一步提升精度。

4. 程序优化与使用便利性

在长期实践中，我对原始实现进行了多项改进：

• 添加详尽注释，提升代码可读性，便于初学者快速掌握逻辑流程；
• 精简冗余结构，提高运行效率；
• 扩展功能模块，支持灵活切换不同分布类型，增强适用范围；
• 统一接口设计，用户仅需替换输入数据文件即可直接运行，极大降低使用门槛。

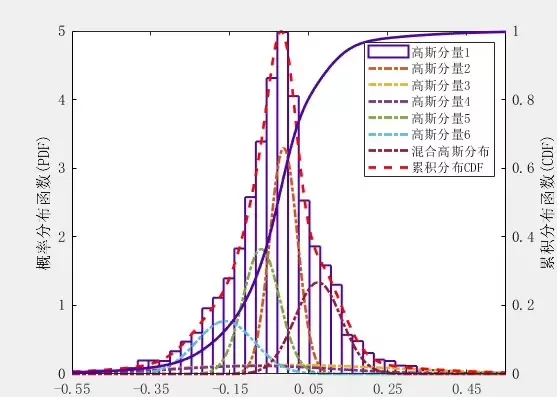
目前版本已集成分布拟合、图表输出、参数导出等多项功能，适用于科研与工程项目的多种需求。

结语

混合高斯模型作为一种灵活且高效的统计工具，在处理非对称、多峰、异方差等复杂分布时表现出色。配合合理的编程实现与后续分析手段，能够在新能源预测、系统建模、数据分析等多个领域发挥关键作用。建议读者在实际项目中积极尝试该方法，挖掘其潜在价值。